What Is 2/3 - 1/4 In Fraction
Treneri
May 10, 2025 · 5 min read
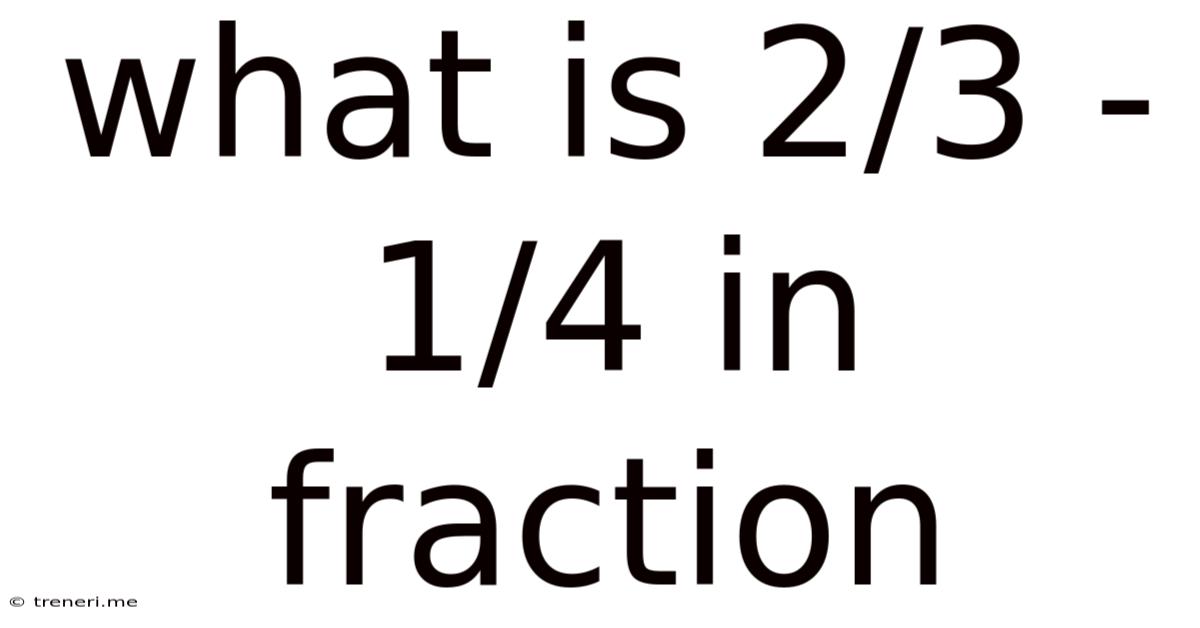
Table of Contents
What is 2/3 - 1/4? A Comprehensive Guide to Fraction Subtraction
Subtracting fractions might seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through subtracting 2/3 - 1/4, explaining the underlying concepts and offering various methods to solve this and similar problems. We’ll delve into the importance of finding a common denominator, simplifying fractions, and even explore real-world applications of fraction subtraction. By the end, you'll confidently tackle any fraction subtraction problem.
Understanding Fractions: A Quick Recap
Before we dive into the subtraction, let's quickly review the fundamental components of a fraction:
- Numerator: The top number in a fraction, representing the number of parts you have.
- Denominator: The bottom number in a fraction, representing the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means you have 2 parts out of a total of 3 equal parts.
Why We Need a Common Denominator
The key to subtracting fractions (and adding them) is to have a common denominator. This means the bottom numbers (denominators) of both fractions must be the same. Why? Imagine trying to subtract apples from oranges – you can't do it directly; you need a common unit of measurement. Similarly, you can't directly subtract fractions with different denominators; you need a common denominator to represent the parts in the same size.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that is a multiple of both denominators. Finding the LCD is crucial for efficient fraction subtraction. There are several ways to find the LCD:
Method 1: Listing Multiples
List the multiples of each denominator until you find the smallest multiple they have in common.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 4: 4, 8, 12, 16, 20...
The smallest common multiple is 12. Therefore, the LCD of 3 and 4 is 12.
Method 2: Prime Factorization
This method is particularly useful for larger denominators. Find the prime factorization of each denominator:
- 3 = 3
- 4 = 2 x 2 = 2²
To find the LCD, take the highest power of each prime factor present in either factorization: 2² x 3 = 12. Therefore, the LCD is 12.
Converting Fractions to a Common Denominator
Once we've found the LCD (which is 12), we need to convert both fractions to equivalent fractions with a denominator of 12. We do this by multiplying both the numerator and the denominator of each fraction by the same number.
-
For 2/3, we multiply both the numerator and denominator by 4 (because 3 x 4 = 12): (2 x 4) / (3 x 4) = 8/12
-
For 1/4, we multiply both the numerator and denominator by 3 (because 4 x 3 = 12): (1 x 3) / (4 x 3) = 3/12
Performing the Subtraction
Now that both fractions have the same denominator, we can subtract the numerators:
8/12 - 3/12 = (8 - 3) / 12 = 5/12
Therefore, 2/3 - 1/4 = 5/12
Simplifying Fractions (If Necessary)
Sometimes, after performing the addition or subtraction, the resulting fraction can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). In this case, 5/12 is already in its simplest form because 5 and 12 have no common divisors other than 1.
Alternative Method: Using Decimal Representation
While less precise for some applications, you can convert the fractions to decimals and then subtract.
- 2/3 ≈ 0.6667
- 1/4 = 0.25
0.6667 - 0.25 = 0.4167
Converting this back to a fraction is more challenging and might result in an approximation, unlike the previous method, which provides the exact fractional result. This method is generally less preferred for maintaining accuracy in mathematical computations, especially in more complex fraction operations.
Real-World Applications of Fraction Subtraction
Fraction subtraction appears in numerous real-life situations:
-
Cooking: Adjusting recipes – If a recipe calls for 2/3 cup of flour and you only have 1/4 cup, you need to find the difference to know how much more you need.
-
Construction: Measuring materials – Cutting a piece of wood to a specific length might involve subtracting fractions of inches or centimeters.
-
Finance: Managing budgets – Tracking expenses and calculating remaining funds often involves subtracting fractions of a dollar.
-
Time Management: Calculating elapsed time – If a task takes 2/3 of an hour and you’ve already spent 1/4 of an hour, you can calculate the remaining time.
Beyond the Basics: Subtracting Mixed Numbers
Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). Subtracting mixed numbers requires an extra step: converting them into improper fractions (fractions where the numerator is larger than the denominator). For example:
Let's subtract 2 1/3 - 1 1/4
-
Convert to improper fractions:
- 2 1/3 = (2 x 3 + 1) / 3 = 7/3
- 1 1/4 = (1 x 4 + 1) / 4 = 5/4
-
Find the LCD: The LCD of 3 and 4 is 12.
-
Convert to a common denominator:
- 7/3 = (7 x 4) / (3 x 4) = 28/12
- 5/4 = (5 x 3) / (4 x 3) = 15/12
-
Subtract: 28/12 - 15/12 = 13/12
-
Convert back to a mixed number (if necessary): 13/12 = 1 1/12
Troubleshooting Common Mistakes
-
Forgetting the common denominator: This is the most common mistake. Always ensure both fractions have the same denominator before subtracting.
-
Incorrectly converting to a common denominator: Double-check your multiplication when converting fractions.
-
Subtracting denominators: Remember, you only subtract the numerators, not the denominators. The denominator remains the same.
-
Not simplifying the answer: Always simplify your final answer to its lowest terms.
Conclusion
Subtracting fractions, while initially seeming complex, becomes manageable with a systematic approach. Mastering the process of finding a common denominator, converting fractions, performing the subtraction, and simplifying the result is key to successfully tackling any fraction subtraction problem, from simple arithmetic to more advanced mixed number operations. Understanding the underlying concepts, practicing regularly, and applying these methods to real-world scenarios will solidify your understanding and build your confidence in working with fractions. Remember to always double-check your work for accuracy and strive for clear and efficient calculations. The methods discussed here will help you conquer fraction subtraction and apply this crucial mathematical skill in various contexts.
Latest Posts
Latest Posts
-
What Is 83 34 Written In Expanded Form
May 10, 2025
-
Find P Value From Chi Square
May 10, 2025
-
How Would You Write 0 0005 In Scientific Notation
May 10, 2025
-
What Is 88k A Year Hourly
May 10, 2025
-
4 5 Divided By 2 3 As A Fraction
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 - 1/4 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.