What Is 3 5 1 3 As A Fraction
Treneri
May 14, 2025 · 5 min read
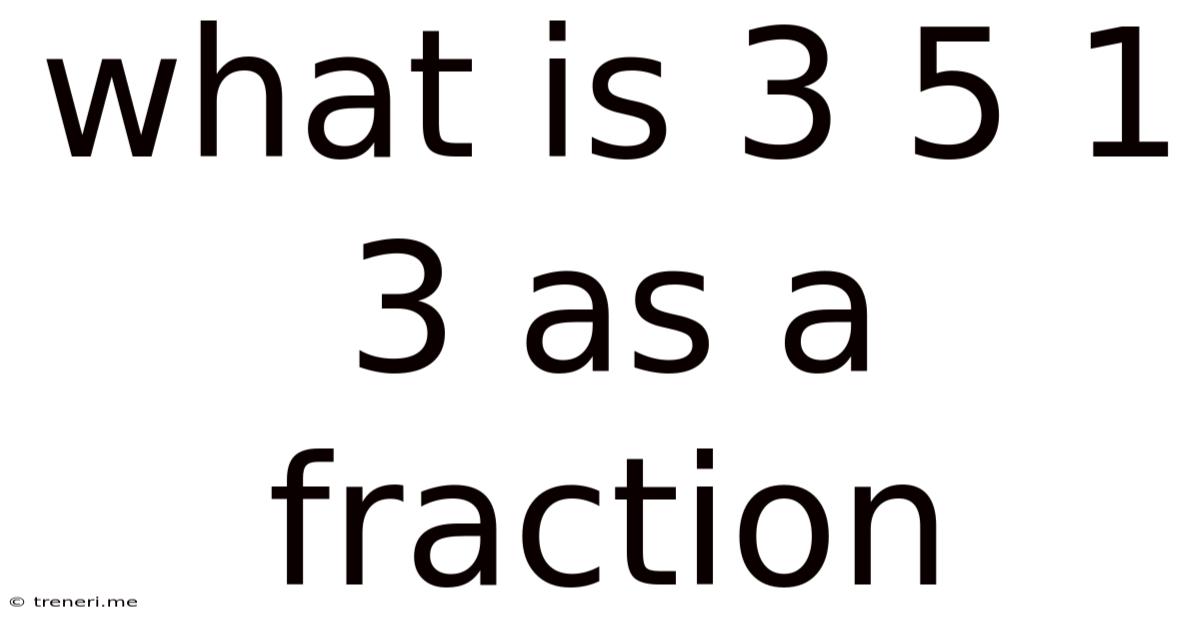
Table of Contents
What is 3 5 1 3 as a Fraction? A Comprehensive Guide to Mixed Numbers and Improper Fractions
The question "What is 3 5 1 3 as a fraction?" might seem simple at first glance, but it delves into the core concepts of mixed numbers, improper fractions, and the crucial process of converting between them. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and tools to tackle similar problems with confidence. We'll explore the underlying mathematical principles and provide practical examples to solidify your understanding.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion, let's clarify the terms involved:
Mixed Numbers: These are numbers that combine a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾, 5 ⅛, and 12 ⅔ are all mixed numbers.
Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator. Examples include ⁵⁄₃, ¹¹⁄₄, and ⁹⁄₉. Improper fractions represent values greater than or equal to one.
The Problem: 3 5 1 3
The expression "3 5 1 3" is not a standard mathematical notation for a mixed number or an improper fraction. It's ambiguous. To interpret it as a fraction, we need to understand what this notation intends to represent. We will explore several possibilities:
Interpretation 1: A Series of Numbers
One possible interpretation is that "3 5 1 3" represents a sequence of numbers. However, without further context or operators (like +, -, ×, ÷), we cannot meaningfully convert this into a single fraction. There's no single, correct fractional representation of simply a list of numbers.
Interpretation 2: Concatenation of Digits
Another interpretation treats "3 5 1 3" as a concatenated number; we string the digits together to form a single integer: 3513. This is not a fraction but a whole number. To convert it to a fraction, we'd write it as ³⁵¹³/₁ (a fraction with denominator 1). This approach is only valid if the intention was to combine these digits as a whole number, not as elements of a fraction or mixed number.
Interpretation 3: Misunderstood Mixed Number Notation
It's highly probable that "3 5 1 3" is an attempt to represent a mixed number but with an unconventional or incorrect format. The proper mixed number notation typically uses a space to separate the whole number from the fraction, as in "3 5/13" or "3 ⅓." It's possible the original expression intended to represent one of these:
-
3 ⁵⁄₁₃: This mixed number represents three whole units and ⁵⁄₁₃ of a unit. To convert it to an improper fraction:
- Multiply the whole number by the denominator: 3 * 13 = 39
- Add the numerator: 39 + 5 = 44
- Keep the same denominator: 44/13
Therefore, 3 ⁵⁄₁₃ as an improper fraction is ⁴⁴⁄₁₃.
-
3 ¹³/₅: This interprets the "5 1 3" portion as the fraction ¹³/₅. This would be another valid (but less probable) interpretation of the original statement, which is more akin to an improperly notated mixed number. To convert to an improper fraction we follow the same steps as above:
- Multiply the whole number by the denominator: 3 * 5 = 15
- Add the numerator: 15 + 13 = 28
- Keep the same denominator: 28/5
Therefore, 3 ¹³/₅ as an improper fraction is ²⁸⁄₅.
Converting Mixed Numbers to Improper Fractions: A Step-by-Step Guide
The process of converting a mixed number to an improper fraction involves these simple steps:
-
Multiply the whole number by the denominator of the fraction: This finds the total number of parts in the whole number portion.
-
Add the numerator of the fraction to the result from step 1: This combines the parts from the whole number and the fractional part.
-
Keep the same denominator: The total number of parts remains the same.
Let's illustrate with an example: Convert 2 ¾ to an improper fraction.
- Multiply the whole number by the denominator: 2 * 4 = 8
- Add the numerator: 8 + 3 = 11
- Keep the same denominator: 11/4
Therefore, 2 ¾ is equivalent to ¹¹⁄₄.
Converting Improper Fractions to Mixed Numbers: The Reverse Process
To convert an improper fraction to a mixed number, perform these steps:
-
Divide the numerator by the denominator: This gives you the whole number part.
-
The remainder becomes the numerator of the fraction: This is the leftover part that didn't make a whole unit.
-
The denominator remains the same: The size of the parts stays consistent.
Example: Convert ¹¹⁄₄ to a mixed number.
- Divide the numerator by the denominator: 11 ÷ 4 = 2 with a remainder of 3
- The remainder becomes the numerator: 3
- The denominator remains the same: 4
Therefore, ¹¹⁄₄ is equivalent to 2 ¾.
Practical Applications and Real-World Examples
Understanding mixed numbers and improper fractions is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Converting between mixed numbers and improper fractions can help in accurately scaling recipes.
-
Construction and Engineering: Precise measurements are crucial in these fields. Working with fractions ensures accuracy in calculations.
-
Finance and Accounting: Dealing with portions of money, interest rates, and shares often requires fractional calculations.
-
Data Analysis: Representing and manipulating data frequently involves working with fractions and proportions.
Conclusion
While the initial question "What is 3 5 1 3 as a fraction?" lacked a precise mathematical representation, it serves as a valuable starting point to delve deeper into the intricacies of mixed numbers and improper fractions. We've seen that the interpretation of "3 5 1 3" depends entirely on how it is meant to be read. We explored possible interpretations, clarified the conversion processes between mixed numbers and improper fractions, and highlighted their real-world relevance. Mastering these concepts will enhance your mathematical skills and problem-solving abilities, preparing you for a wide range of applications. Remember, always ensure the notation is clear and unambiguous to avoid confusion in any calculations involving fractions and mixed numbers.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 36 And 63
May 14, 2025
-
1 10000 As A Power Of 10
May 14, 2025
-
What Is The Gcf Of 12 36
May 14, 2025
-
70 Inches Is How Many Meters
May 14, 2025
-
What Is The Gcf Of 12 18 And 24
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 5 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.