1/10000 As A Power Of 10
Treneri
May 14, 2025 · 5 min read
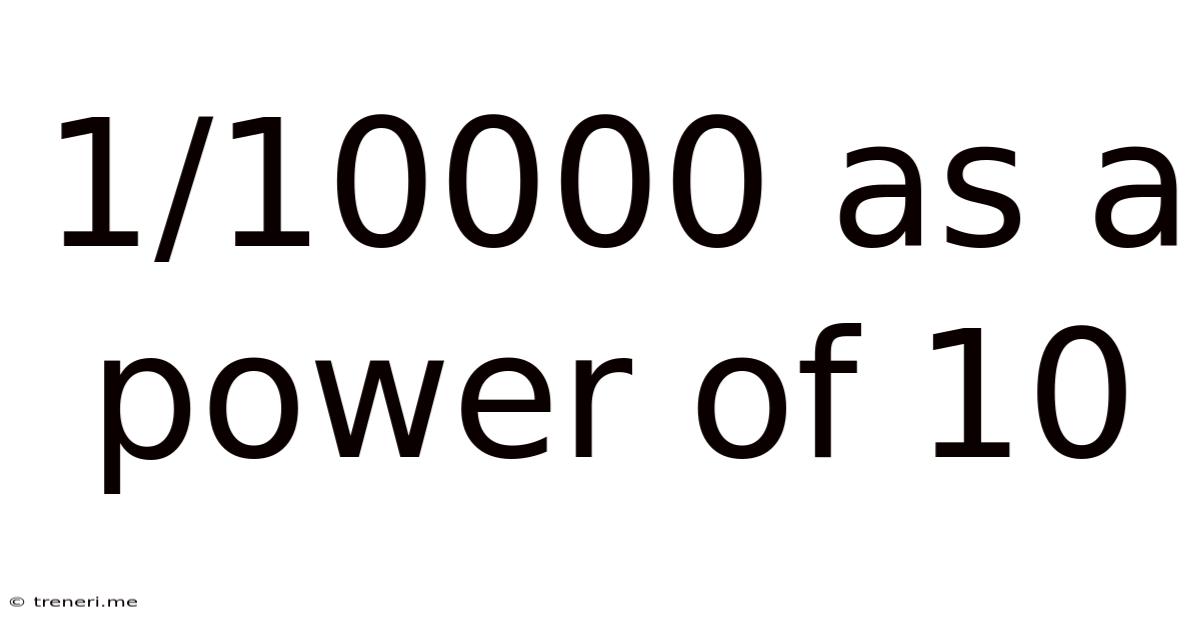
Table of Contents
1/10000 as a Power of 10: Exploring Exponential Notation and its Applications
Understanding exponential notation, particularly representing fractions as powers of 10, is fundamental to various fields, from scientific notation to computer programming. This comprehensive article delves into the representation of 1/10000 as a power of 10, exploring the underlying principles, practical applications, and broader implications of working with negative exponents.
Defining Exponential Notation
Exponential notation, also known as scientific notation or standard form, provides a concise way to express very large or very small numbers. It involves writing a number in the form a × 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer representing the exponent or power of 10. The exponent indicates how many places the decimal point needs to be moved to obtain the original number.
A positive exponent signifies a large number (greater than 1), while a negative exponent indicates a small number (between 0 and 1). This is crucial for understanding fractions expressed as powers of 10.
Expressing 1/10000 as a Power of 10
The fraction 1/10000 can be rewritten as a decimal: 0.0001. To express this as a power of 10, we need to determine the exponent that shifts the decimal point to create the number 1.
We can see that moving the decimal point four places to the right gives us 1. Since we moved the decimal point to the right, the exponent will be negative. Therefore, 0.0001 can be written as 10<sup>-4</sup>.
In summary:
1/10000 = 0.0001 = 10<sup>-4</sup>
Understanding Negative Exponents
Negative exponents represent the reciprocal of the positive power of 10. In simpler terms:
10<sup>-n</sup> = 1/10<sup>n</sup>
This means that 10<sup>-4</sup> is equivalent to 1/(10<sup>4</sup>), which is 1/10000. This relationship is fundamental to understanding how small fractions are represented in exponential notation. It elegantly handles numbers much smaller than 1 without cumbersome decimal expansions.
Practical Applications of Exponential Notation
The ability to express numbers as powers of 10 has far-reaching applications across various disciplines:
1. Scientific Notation in Physics and Chemistry:
Scientific notation is widely used in science to express extremely large or small quantities, such as the mass of an electron (approximately 9.109 × 10<sup>-31</sup> kilograms) or the distance to a distant star (potentially measured in light-years, a very large number). It simplifies calculations and improves readability when dealing with extreme values.
2. Computer Science and Data Representation:
Computers work with binary numbers (base-2), but powers of 10 are often used to represent data sizes in units such as kilobytes (KB), megabytes (MB), gigabytes (GB), and terabytes (TB). Each unit represents a power of 1024 (2<sup>10</sup>), which is approximately 10<sup>3</sup>, reflecting the relationship between decimal and binary systems. Understanding powers of 10 is essential for interpreting and manipulating digital data effectively.
3. Financial Calculations and Compound Interest:
In finance, exponential notation helps in calculations related to compound interest. The formula for compound interest involves exponents, allowing for the precise determination of future investment values over extended periods. Understanding negative exponents is relevant when considering discounting future cash flows.
4. Engineering and Scaling:
Engineers frequently use powers of 10 to represent scaling factors in designs. Whether it's designing microchips with dimensions in nanometers or constructing large-scale infrastructure projects, understanding exponential notation is crucial for precise measurements and calculations at various scales.
5. Mathematics and Calculus:
Powers of 10 are integral to many mathematical concepts, including logarithms, limits, and derivatives. The ability to manipulate and interpret numbers expressed in exponential notation simplifies complex mathematical calculations and problem-solving.
Further Exploration of Powers of 10
The concept of expressing numbers as powers of 10 extends beyond just positive and negative integers. It also encompasses fractional exponents, which represent roots:
- 10<sup>1/2</sup> represents the square root of 10 (approximately 3.162).
- 10<sup>1/3</sup> represents the cube root of 10 (approximately 2.154).
These fractional exponents further expand the versatility of exponential notation, allowing the representation of a wider range of numbers with precision and clarity.
Advanced Applications: Logarithmic Scales
Logarithmic scales, such as the Richter scale for earthquakes or the decibel scale for sound intensity, use powers of 10 to represent a wide range of values in a compressed manner. They are extremely helpful when visualizing data with vast ranges, as they allow for a more manageable and interpretable representation. Understanding negative exponents is crucial for interpreting values at the lower end of logarithmic scales.
Working with Powers of 10: Key Principles
Several key principles govern the manipulation of numbers expressed as powers of 10:
- Multiplication: When multiplying numbers in exponential notation, you add the exponents. For example: 10<sup>3</sup> × 10<sup>2</sup> = 10<sup>(3+2)</sup> = 10<sup>5</sup>
- Division: When dividing numbers in exponential notation, you subtract the exponents. For example: 10<sup>5</sup> / 10<sup>2</sup> = 10<sup>(5-2)</sup> = 10<sup>3</sup>
- Powers of Powers: When raising a power of 10 to another power, you multiply the exponents. For example: (10<sup>3</sup>)<sup>2</sup> = 10<sup>(3×2)</sup> = 10<sup>6</sup>
Mastering these rules is fundamental to performing accurate calculations involving powers of 10.
Conclusion: The Importance of 10<sup>-4</sup> and Beyond
Representing 1/10000 as 10<sup>-4</sup> is not just a mathematical curiosity; it's a cornerstone of scientific, computational, and engineering practices. The ability to express numbers using exponential notation significantly simplifies calculations, improves data representation, and enhances our understanding of vastly different scales of magnitude, from the subatomic to the cosmological. Understanding and applying these principles, particularly the use of negative exponents, is crucial for anyone working with numerical data across diverse fields. Through its concise representation, 10<sup>-4</sup>, and other powers of 10, provide a powerful tool for effectively handling both extremely small and extremely large numbers. This enables better comprehension of complex phenomena and facilitates more precise computations. The broader implications extend to numerous applications across various scientific and technological fields.
Latest Posts
Latest Posts
-
4 5 Divided By 2 3 As A Fraction
May 14, 2025
-
What Fraction Is Equivalent To 8 10
May 14, 2025
-
Cuanto Es 10 Libras En Kilogramos
May 14, 2025
-
60 Out Of 70 Is What Percent
May 14, 2025
-
How Much Longer Until 4 Pm Today
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1/10000 As A Power Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.