What Is 3 Percent Of 400
Treneri
May 10, 2025 · 5 min read
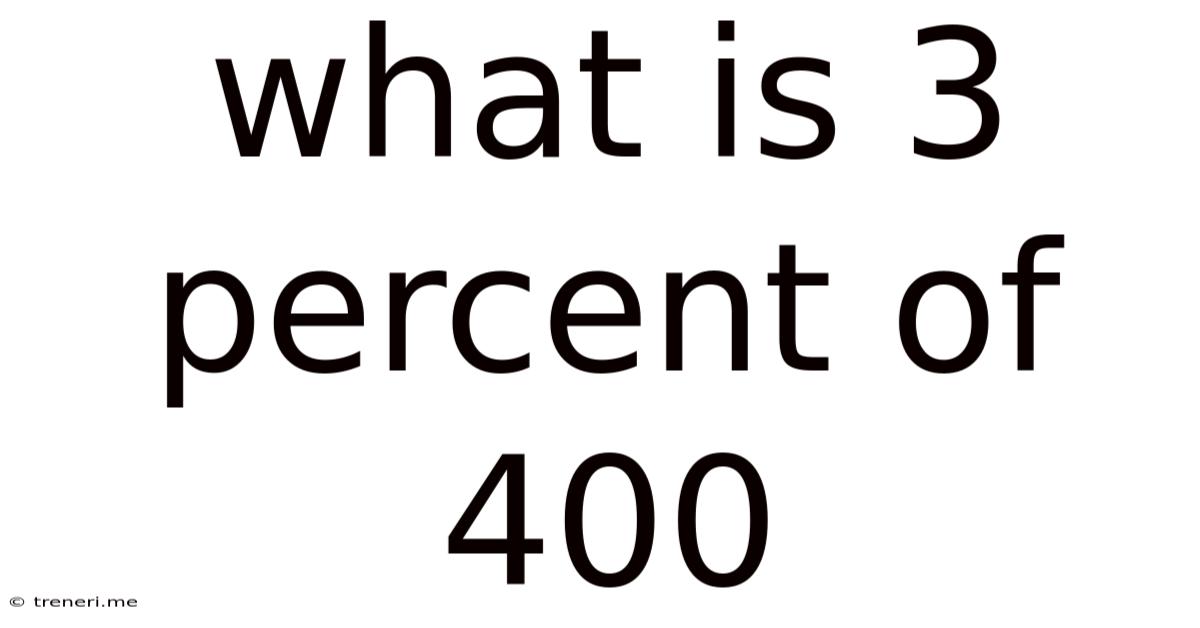
Table of Contents
What is 3 Percent of 400? A Deep Dive into Percentages and Their Applications
Finding 3 percent of 400 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from budgeting and finance to sales, discounts, and even scientific calculations. This article will not only answer the question directly but also explore the various methods for calculating percentages, their practical uses, and how to confidently tackle more complex percentage problems.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The term "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 3 percent (written as 3%) means 3 out of every 100. This fundamental understanding is key to solving any percentage problem.
Key Concepts:
- Percentage: The portion of a whole expressed as a number out of 100.
- Whole: The total amount or quantity you're considering.
- Part: The portion of the whole represented by the percentage.
Calculating 3 Percent of 400: Three Methods
There are several ways to calculate 3% of 400. Let's explore the most common methods:
Method 1: Converting Percentage to a Decimal
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the whole number.
- Convert the percentage to a decimal: 3% is equal to 3/100 = 0.03.
- Multiply the decimal by the whole number: 0.03 * 400 = 12
Therefore, 3% of 400 is 12.
Method 2: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying it by the whole number.
- Convert the percentage to a fraction: 3% is equal to 3/100.
- Multiply the fraction by the whole number: (3/100) * 400 = 12
Again, we arrive at the answer: 3% of 400 is 12.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve the problem. We set up a proportion where one ratio represents the percentage and the other represents the unknown part relative to the whole.
- Set up a proportion: 3/100 = x/400 (where x is the unknown value we're trying to find).
- Cross-multiply: 100x = 3 * 400
- Solve for x: 100x = 1200 => x = 1200/100 = 12
Once more, we find that 3% of 400 is 12.
Practical Applications of Percentages: Real-World Examples
The ability to calculate percentages is crucial in many real-world situations. Let's explore a few examples:
1. Sales and Discounts:
Imagine a store offering a 3% discount on a $400 item. Using our knowledge, the discount amount is $12, and the final price would be $400 - $12 = $388. Understanding percentages allows consumers to quickly determine the final cost after a discount.
2. Taxes and Tips:
Calculating sales tax or service tips often involves percentages. If the sales tax is 6% on a $400 purchase, the tax amount would be 0.06 * $400 = $24. Similarly, calculating a 15% tip on a $400 restaurant bill is a straightforward percentage calculation.
3. Finance and Investments:
Percentages are fundamental in finance. Interest rates, returns on investment, and inflation are all expressed as percentages. Understanding percentage changes helps investors track the performance of their portfolios and make informed decisions. For instance, calculating the interest earned on a savings account or the growth of an investment over time relies heavily on percentage calculations.
4. Data Analysis and Statistics:
In data analysis and statistics, percentages are used to represent proportions and trends within datasets. For example, expressing survey results, market share, or population demographics often involves percentages. Understanding percentages is critical for interpreting data and drawing meaningful conclusions.
5. Science and Engineering:
Percentages are employed extensively in scientific and engineering fields. Calculating efficiency rates, error margins, or expressing concentrations of substances all involve percentage calculations. For example, determining the percentage purity of a chemical compound or the efficiency of a solar panel relies on understanding and accurately calculating percentages.
Tackling More Complex Percentage Problems: Advanced Techniques
While finding 3% of 400 is relatively simple, more complex percentage problems might require additional steps. Here are some strategies for tackling these challenges:
1. Finding the Percentage One Number Represents of Another:
Let's say you sold 120 items out of 400. To find the percentage of items sold, you would divide the number sold by the total number of items and then multiply by 100: (120/400) * 100 = 30%.
2. Finding the Original Whole from a Percentage:
If you know that 12 represents 3% of a certain number, you can find the original number by dividing 12 by 0.03: 12 / 0.03 = 400.
3. Calculating Percentage Increase or Decrease:
To calculate a percentage increase or decrease, you first find the difference between the two numbers, then divide the difference by the original number, and finally multiply by 100. For example, if a price increased from $200 to $250, the percentage increase is (($250 - $200) / $200) * 100 = 25%.
Conclusion: Mastering Percentages for Success
The seemingly simple calculation of 3% of 400 opens the door to a vast world of practical applications. From everyday shopping to complex financial decisions, mastering percentages is a vital skill. By understanding the fundamental concepts and employing the different calculation methods, you can confidently tackle a wide array of percentage problems and effectively utilize this critical tool in various aspects of your life. Remember to practice regularly, and you'll soon find yourself effortlessly navigating the world of percentages. This comprehensive understanding will empower you to make informed decisions, analyze data effectively, and solve problems accurately across numerous fields.
Latest Posts
Latest Posts
-
What Is 4 3 Divided By 5 3
May 10, 2025
-
Does One Ml Equal One Gram
May 10, 2025
-
What Is 25 Of 2 Million
May 10, 2025
-
How Much Is 2 Yards Of Sand
May 10, 2025
-
How Tall Is 104 Cm In Feet
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.