What Is 4/5 Divided By 1/10
Treneri
May 11, 2025 · 5 min read
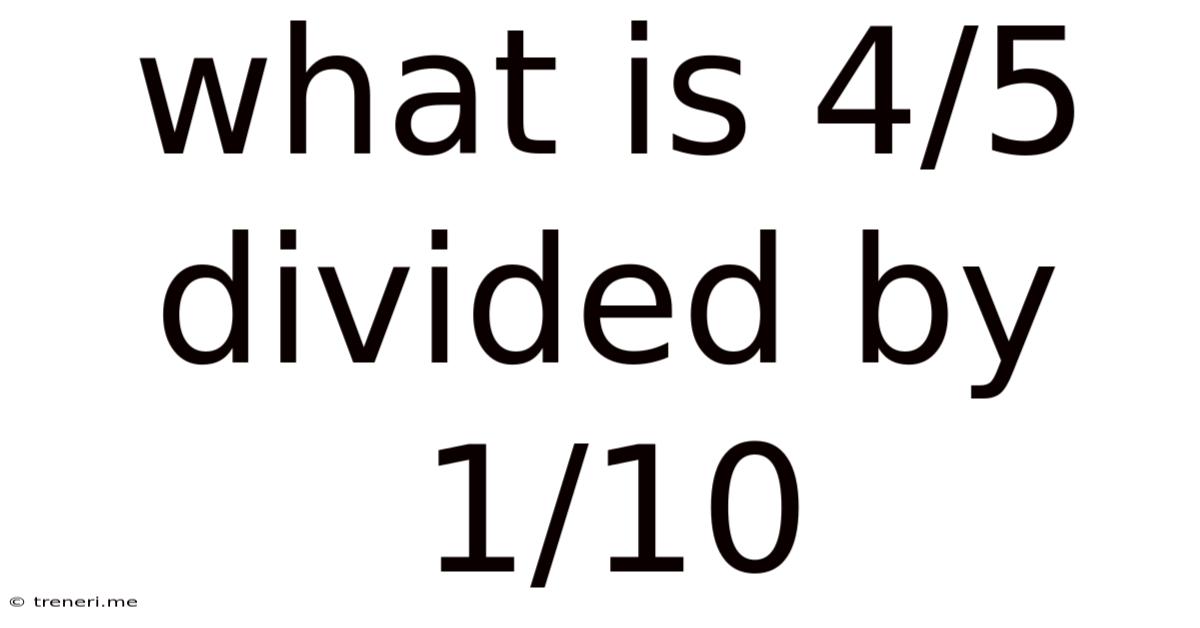
Table of Contents
What is 4/5 Divided by 1/10? A Deep Dive into Fraction Division
The seemingly simple question, "What is 4/5 divided by 1/10?" opens the door to a deeper understanding of fraction division, a crucial concept in mathematics with far-reaching applications in various fields. This comprehensive guide will not only provide the solution but also delve into the underlying principles, offer alternative methods, and explore practical real-world examples.
Understanding Fraction Division
Before tackling the specific problem, let's establish a solid foundation in fraction division. Unlike addition and subtraction, where we need common denominators, dividing fractions involves a different approach: we invert (or find the reciprocal of) the second fraction and then multiply. This process is encapsulated in the following rule:
a/b ÷ c/d = a/b × d/c
Where 'a', 'b', 'c', and 'd' represent numbers, and 'b' and 'c' are not zero (division by zero is undefined).
This rule stems from the fundamental concept of division as the inverse of multiplication. Dividing by a fraction is equivalent to multiplying by its reciprocal. Consider the following analogy: Dividing a pizza into 4 slices and then dividing one slice further into 2 smaller pieces is equivalent to dividing the whole pizza into 8 smaller pieces. This inverse relationship is what underpins our method for dividing fractions.
Solving 4/5 Divided by 1/10
Now, let's apply this knowledge to our problem: 4/5 ÷ 1/10.
Following the rule:
4/5 ÷ 1/10 = 4/5 × 10/1
We now multiply the numerators together and the denominators together:
(4 × 10) / (5 × 1) = 40/5
Finally, we simplify the resulting fraction:
40/5 = 8
Therefore, 4/5 divided by 1/10 equals 8.
Alternative Methods and Visualizations
While the "invert and multiply" method is the most efficient, understanding alternative approaches can solidify your comprehension.
Using Common Denominators
Although less common for division, we can find a common denominator and express the division as a fraction of fractions:
4/5 ÷ 1/10 can be rewritten as (4/5) / (1/10)
To simplify this complex fraction, we can multiply both the numerator and denominator by the least common multiple (LCM) of the denominators (which is 10 in this case):
[(4/5) × 10] / [(1/10) × 10] = 8/1 = 8
This method demonstrates that the result remains consistent regardless of the approach.
Visual Representation
Visualizing the problem can be particularly helpful. Imagine you have a chocolate bar divided into 5 equal pieces (representing 4/5 of the bar). If you want to divide this 4/5 into portions that are 1/10 of the whole bar, how many portions do you have?
Consider dividing each of the 5 sections of the original bar into 2 smaller pieces (creating a total of 10). You now have 8 of these smaller pieces from your original 4/5. Hence, the answer remains 8.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various professions:
Cooking and Baking
Recipes often require dividing ingredients. For instance, if a recipe calls for 4/5 of a cup of flour and you only want to make 1/10 of the recipe, you would need to calculate 4/5 ÷ 10 to find the amount of flour needed.
Sewing and Tailoring
Tailors and seamstresses regularly use fraction division to calculate fabric requirements. If a pattern calls for 2 1/2 yards of fabric, and you need to make a smaller version that's 1/3 the size, you'd use fraction division to determine the reduced fabric amount.
Construction and Engineering
Precise measurements are crucial in construction and engineering. Dividing materials or calculating distances often involves fraction division, ensuring accuracy in projects.
Data Analysis and Statistics
In data analysis and statistics, fractions and ratios are frequently used. Understanding fraction division is essential for interpreting results and making informed decisions.
Advanced Concepts and Extensions
While we've focused on simple fractions, the principles of fraction division extend to more complex scenarios:
Dividing Mixed Numbers
Mixed numbers (numbers that consist of a whole number and a fraction, like 2 1/3) require conversion to improper fractions before applying the division rule.
Dividing Fractions with Variables
The same principles apply to fractions containing variables (letters representing unknown numbers). The process of inverting and multiplying remains the same, but the resulting expression will often contain variables.
Applications in Algebra and Calculus
Fraction division forms the basis for numerous operations in higher-level mathematics, including algebraic manipulations and calculus computations.
Conclusion: Mastering Fraction Division
Understanding how to divide fractions, and specifically solving problems like 4/5 divided by 1/10, is a fundamental skill with widespread applicability. By mastering this concept, you'll enhance your mathematical proficiency, improve problem-solving abilities, and gain a deeper appreciation for the interconnectedness of mathematical principles across diverse fields. Remember the key rule: invert and multiply! And don't hesitate to explore different methods and visualize the problem to cement your understanding. With practice, fraction division will become second nature. This comprehensive guide, enriched with examples and practical applications, has hopefully equipped you with a robust understanding of this crucial mathematical skill. Remember to continue practicing and exploring different problems to build your confidence and mastery.
Latest Posts
Latest Posts
-
Can You Tan At Uv 7
May 12, 2025
-
900 Days Is How Many Years
May 12, 2025
-
0 2 Of What Number Is 8
May 12, 2025
-
Si Naci En 1967 Cuantos Anos Tengo En El 2024
May 12, 2025
-
Find The Tension In Rope A
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/5 Divided By 1/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.