What Is 5/10 As A Percentage
Treneri
May 11, 2025 · 5 min read
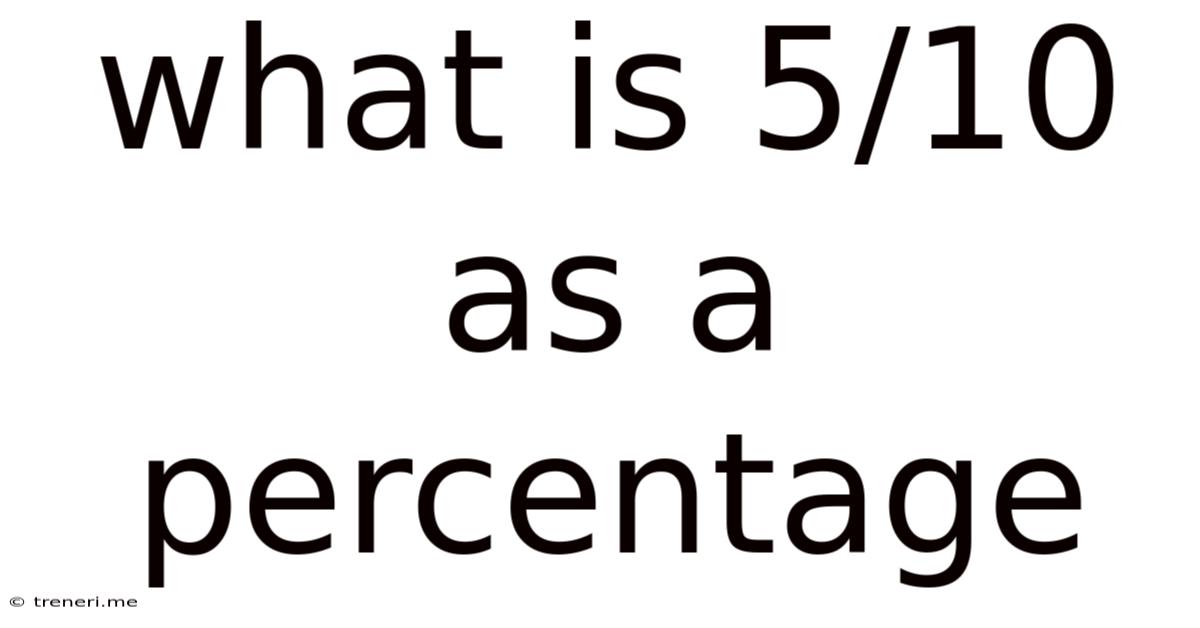
Table of Contents
What is 5/10 as a Percentage? A Comprehensive Guide
Fractions and percentages are fundamental concepts in mathematics with widespread applications in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 5/10 into a percentage, explaining the underlying principles and providing practical examples. We’ll also explore related concepts and answer frequently asked questions, ensuring a thorough understanding of this essential mathematical skill.
Understanding Fractions and Percentages
Before we convert 5/10 to a percentage, let's clarify the core concepts:
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole. For example, in the fraction 5/10, 5 is the numerator and 10 is the denominator.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100". Percentages are denoted by the symbol "%". For example, 25% means 25 out of 100, or 25/100.
Converting 5/10 to a Percentage: Step-by-Step
The conversion of a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert the fraction 5/10 to a decimal, we simply divide the numerator (5) by the denominator (10):
5 ÷ 10 = 0.5
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.5 × 100 = 50%
Therefore, 5/10 is equal to 50%.
Alternative Method: Simplifying the Fraction First
Alternatively, we can simplify the fraction 5/10 before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 5 and 10 is 5:
5 ÷ 5 = 1 10 ÷ 5 = 2
This simplifies the fraction to 1/2. Now, we can convert 1/2 to a decimal:
1 ÷ 2 = 0.5
And then convert the decimal to a percentage:
0.5 × 100 = 50%
This demonstrates that simplifying the fraction first doesn't change the final percentage. Both methods yield the same result: 50%.
Real-world Applications of 5/10 (50%)
The concept of 50% appears frequently in various real-world situations:
- Sales and Discounts: A 50% discount means you pay half the original price. If an item costs $100, a 50% discount reduces the price to $50.
- Statistics and Probability: 50% represents a probability of one half, often used to express the likelihood of an event occurring. For example, flipping a fair coin has a 50% chance of landing on heads.
- Grades and Assessments: In many educational systems, 50% might represent the minimum passing grade.
- Financial Investments: Understanding percentages is crucial for calculating returns on investments, interest rates, and other financial metrics. A 50% return on an investment means your investment has doubled.
- Data Analysis: Percentages are used extensively in data analysis to represent proportions and trends within datasets.
Further Exploration: Working with Other Fractions and Percentages
The process of converting fractions to percentages is applicable to any fraction. Let's look at a few more examples:
Example 1: Converting 3/4 to a percentage
- Convert to a decimal: 3 ÷ 4 = 0.75
- Convert to a percentage: 0.75 × 100 = 75%
Therefore, 3/4 is equal to 75%.
Example 2: Converting 1/5 to a percentage
- Convert to a decimal: 1 ÷ 5 = 0.2
- Convert to a percentage: 0.2 × 100 = 20%
Therefore, 1/5 is equal to 20%.
Example 3: Converting 7/8 to a percentage
- Convert to a decimal: 7 ÷ 8 = 0.875
- Convert to a percentage: 0.875 × 100 = 87.5%
Therefore, 7/8 is equal to 87.5%.
Frequently Asked Questions (FAQs)
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare different quantities, making it easier to understand proportions and make informed decisions in various contexts, from shopping to finance to data analysis.
Q: Can I convert a percentage back to a fraction?
A: Yes, to convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Q: What if the fraction has a larger numerator than denominator?
A: If the numerator is larger than the denominator (an improper fraction), the resulting percentage will be greater than 100%. For example, 5/2 = 2.5, which converts to 250%.
Q: Are there any online tools to help with fraction to percentage conversion?
A: While many online calculators exist, mastering the manual process is valuable for understanding the underlying mathematical concepts.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting fractions to percentages is a crucial skill with broad applications in various fields. Understanding the underlying principles, as demonstrated through the step-by-step conversion of 5/10 to 50% and the examples provided, is essential for navigating various mathematical and real-world situations. This comprehensive guide equipped you with the knowledge and tools to confidently tackle these conversions and leverage percentages in your daily life and professional endeavors. Remember the simple steps, practice regularly, and you’ll quickly become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Find The Area Of The Following Shape
May 12, 2025
-
17 Divided By 3 With Remainder
May 12, 2025
-
13 Out Of 18 As A Grade
May 12, 2025
-
What Is The Percentage Of 12 Out Of 16
May 12, 2025
-
5 3 4 As A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 5/10 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.