What Is 6 2/3 In Radical Form
Treneri
May 10, 2025 · 4 min read
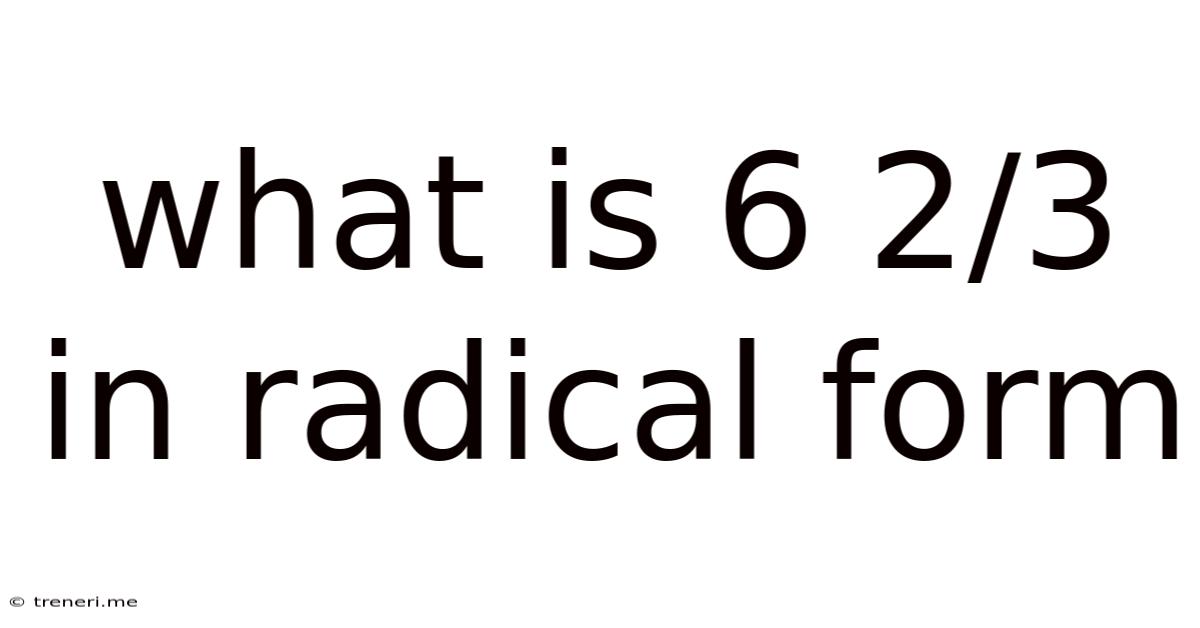
Table of Contents
What is 6 2/3 in Radical Form? A Comprehensive Guide
The question, "What is 6 2/3 in radical form?" might seem straightforward at first glance. However, understanding the process requires a solid grasp of fraction manipulation, exponent rules, and the very definition of radicals. This comprehensive guide will not only answer this specific question but also equip you with the knowledge to tackle similar problems involving the conversion of mixed numbers into radical expressions.
Understanding the Fundamentals
Before diving into the conversion, let's review the fundamental concepts:
1. Mixed Numbers and Improper Fractions:
A mixed number, like 6 2/3, represents a whole number and a fraction. To work with it effectively in radical form, we must first convert it into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
To convert 6 2/3 to an improper fraction:
- Multiply the whole number (6) by the denominator (3): 6 * 3 = 18
- Add the numerator (2) to the result: 18 + 2 = 20
- Keep the same denominator (3): The improper fraction is 20/3.
2. Exponents and Radicals:
Exponents indicate repeated multiplication. For example, 2³ = 2 * 2 * 2 = 8.
A radical (√) is the opposite of an exponent. It represents the root of a number. The number above the radical symbol (the index) indicates which root to find. For example:
- √9 (square root of 9) = 3 because 3 * 3 = 9
- ³√8 (cube root of 8) = 2 because 2 * 2 * 2 = 8
The relationship between exponents and radicals is crucial: a fractional exponent can be expressed as a radical. Specifically:
x^(m/n) = ⁿ√(xᵐ)
Where:
- x is the base
- m is the exponent in the numerator
- n is the exponent in the denominator
This relationship is the key to converting our improper fraction into radical form.
Converting 6 2/3 to Radical Form
Now, let's apply these concepts to convert 6 2/3 (or 20/3) into radical form.
- Rewrite the improper fraction as an exponent:
The improper fraction 20/3 can be written as 20 raised to the power of 1/3: 20^(1/3)
- Express the fractional exponent as a radical:
Using the relationship x^(m/n) = ⁿ√(xᵐ), we can rewrite 20^(1/3) as:
³√20
Therefore, 6 2/3 in radical form is ³√20. This represents the cube root of 20. There's no further simplification possible because 20 does not have any perfect cube factors other than 1.
Extending the Concept: Other Examples and Considerations
Let's explore other examples to solidify your understanding. Consider the mixed number 4 1/2:
-
Convert to an improper fraction: (4 * 2) + 1 = 9. The improper fraction is 9/2.
-
Rewrite as an exponent: 9^(1/2)
-
Express as a radical: √9 = 3
Therefore, 4 1/2 in radical form simplifies to 3. This illustrates that simplification is possible if the number under the radical has perfect square factors.
Dealing with Larger Numbers and Indices:
What if we have a more complex mixed number, such as 10 3/4?
-
Convert to an improper fraction: (10 * 4) + 3 = 43. The improper fraction is 43/4.
-
Rewrite as an exponent: 43^(1/4)
-
Express as a radical: ⁴√43
In this case, 43 does not have any perfect fourth-power factors, so ⁴√43 is the simplest radical form.
Handling Negative Exponents:
The principles remain consistent even if the fractional exponent is negative. Recall that x^(-m/n) = 1/(x^(m/n)).
For example, let's convert the mixed number 2 1/3 into its radical form using a negative exponent:
-
Convert to an improper fraction: (2 * 3) + 1 = 7/3
-
Rewrite with a negative exponent: 7^(-1/3)
-
Express as a radical (using the reciprocal rule): 1/(³√7)
This demonstrates how the negative exponent introduces a reciprocal into the radical expression.
Practical Applications and Further Exploration
The conversion of mixed numbers into radical form has applications in various mathematical fields, including:
- Algebra: Simplifying expressions involving radicals and exponents.
- Calculus: Evaluating limits and derivatives involving radical functions.
- Geometry: Calculating lengths and areas using radical expressions.
- Physics and Engineering: Solving equations involving radical expressions.
This comprehensive guide provides a foundation for understanding the conversion of mixed numbers into radical form. By mastering the principles of fraction manipulation, exponent rules, and the relationship between exponents and radicals, you'll be equipped to tackle a wide range of problems involving these concepts. Remember that the key is to break down the problem into manageable steps, starting with converting the mixed number into an improper fraction, then expressing it as a fractional exponent, and finally writing the result in its simplest radical form. Practice with various examples will further strengthen your understanding and build your confidence in handling radical expressions.
Latest Posts
Latest Posts
-
1 2 X 1 3 As A Fraction
May 10, 2025
-
30 Days After November 6 2024
May 10, 2025
-
90 Days From April 7 2024
May 10, 2025
-
How Many Ounces In 88 Grams
May 10, 2025
-
Under 2 Hours Half Marathon Pace
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 2/3 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.