What Is 60 Percent Of 8
Treneri
Apr 03, 2025 · 5 min read
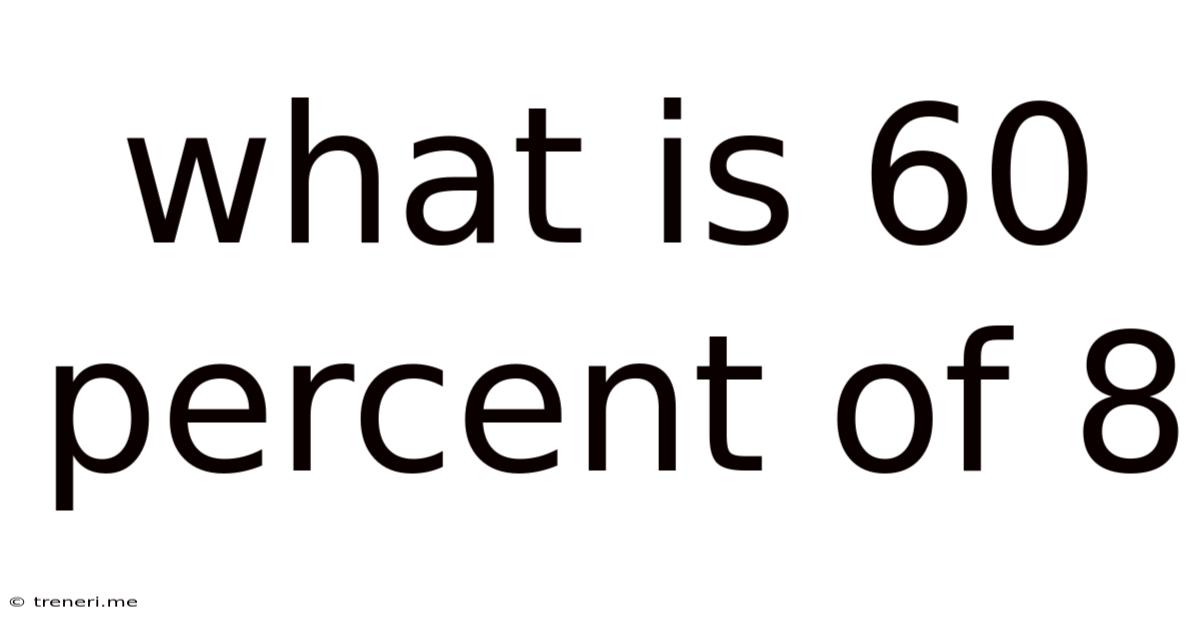
Table of Contents
What is 60 Percent of 8? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 8 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer the question directly but will also explore the underlying principles of percentages, different methods for calculating them, and real-world examples showcasing their importance.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 60 percent means 60 out of 100, or 60/100. This fraction can be simplified to 3/5. Understanding this fundamental concept is crucial for grasping percentage calculations.
Key Concepts:
- Percentage: A number or ratio expressed as a fraction of 100.
- Whole Number: The total amount or quantity you're taking a percentage of (in our case, 8).
- Part: The portion of the whole number represented by the percentage (what we need to calculate).
Calculating 60 Percent of 8: Three Methods
There are several ways to calculate 60 percent of 8. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. First, convert the percentage to a decimal by dividing it by 100:
60% ÷ 100 = 0.60
Then, multiply the decimal by the whole number:
0.60 * 8 = 4.8
Therefore, 60 percent of 8 is 4.8.
Method 2: Using the Fraction Equivalent
As mentioned earlier, 60% can be expressed as the fraction 3/5. To find 60% of 8, we multiply the fraction by the whole number:
(3/5) * 8 = 24/5
Now, convert the improper fraction to a decimal by dividing the numerator by the denominator:
24 ÷ 5 = 4.8
Again, we arrive at the answer: 4.8.
Method 3: Using Proportions
This method is particularly helpful for understanding the relationship between percentages and their corresponding parts. We can set up a proportion:
60/100 = x/8
Where 'x' represents the unknown value (60% of 8). To solve for 'x', we cross-multiply:
60 * 8 = 100 * x
480 = 100x
x = 480/100
x = 4.8
This confirms our previous calculations: 60 percent of 8 is 4.8.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world scenarios. Here are a few examples:
1. Discounts and Sales:
Stores frequently offer discounts on goods. For example, a 60% discount on an item priced at $8 would mean a reduction of $4.80 (60% of $8). This calculation helps consumers determine the final price after the discount is applied. Understanding discounts allows consumers to make informed purchasing decisions and compare deals across different retailers. This application of percentages is crucial for financial literacy.
2. Taxes and Tips:
Sales tax is typically expressed as a percentage. Calculating the tax amount involves finding a percentage of the total purchase price. Similarly, calculating a tip in a restaurant often involves determining a percentage of the bill. This knowledge directly impacts personal finances and budgeting. Understanding tax calculations is vital for accurate financial record-keeping.
3. Interest Rates and Investments:
Interest rates on loans and savings accounts are usually expressed as percentages. This knowledge is crucial for understanding the cost of borrowing money or the potential earnings from investments. Calculating interest earned or paid involves finding a percentage of the principal amount. This directly impacts investment decisions and financial planning.
4. Statistical Analysis and Data Interpretation:
Percentages are extensively used in statistical analysis to represent proportions and ratios within datasets. For instance, if a survey shows that 60% of respondents prefer a particular product, this provides valuable insights into market trends and consumer preferences. This application is crucial for making informed decisions in marketing, product development, and business strategy.
5. Grade Calculations:
In many educational systems, grades are often calculated as percentages of total possible points. For instance, if a student scores 4.8 out of 8 on a quiz, their score translates to 60% (4.8/8 * 100). This helps students understand their performance and progress in a particular subject. Grade calculations form a fundamental part of academic assessment and performance evaluation.
Advanced Percentage Calculations: Extending the Concept
While calculating 60% of 8 is relatively simple, the principles involved extend to more complex calculations:
1. Finding the Percentage One Number Represents of Another:
Suppose you have scored 6 out of 8 on a test. To find the percentage, you would divide the score by the total possible points and multiply by 100:
(6/8) * 100 = 75%
This indicates you scored 75% on the test. This application is crucial in various assessment methods and evaluations.
2. Finding the Original Amount Given a Percentage and its Value:
If you know that 60% of a certain amount is 4.8, you can work backward to find the original amount. This often requires setting up an equation and solving for the unknown variable.
0.60 * x = 4.8
x = 4.8 / 0.60
x = 8
This confirms the original amount was 8. This type of calculation is crucial in reverse engineering pricing and discount structures.
3. Calculating Percentage Increase or Decrease:
Percentage change is frequently used to analyze trends and variations over time. The formula for percentage increase or decrease is:
[(New Value - Old Value) / Old Value] * 100
For instance, if a value increases from 8 to 10, the percentage increase is:
[(10 - 8) / 8] * 100 = 25%
This ability to calculate percentage change is crucial for interpreting data and analyzing trends in business, economics, and many other fields.
Conclusion: The Ubiquity of Percentages
This exploration shows that the simple calculation of "what is 60 percent of 8?" serves as a gateway to a vast world of mathematical applications. From everyday shopping to complex financial analyses, understanding percentages is a vital skill that empowers individuals to make informed decisions, interpret data effectively, and navigate various aspects of modern life. Mastering percentage calculations equips individuals with a powerful tool for problem-solving and critical thinking across numerous domains. The fundamental principles discussed here provide a strong foundation for tackling more advanced percentage-related calculations and applications in the future. Remember, practice makes perfect, so continue exploring various examples and applications to solidify your understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
Cuantos Dias Faltan Para El 10 De Junio
May 09, 2025
-
11 Pound Ham Feeds How Many
May 09, 2025
-
Tabla De Calorias Completa Y Peso Ideal
May 09, 2025
-
How To Find The Center Of A Sphere
May 09, 2025
-
4 Is 20 Percent Of What Number
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.