What Is 8/12 - 4/8 Reduced To The Lowest Terms
Treneri
May 11, 2025 · 5 min read
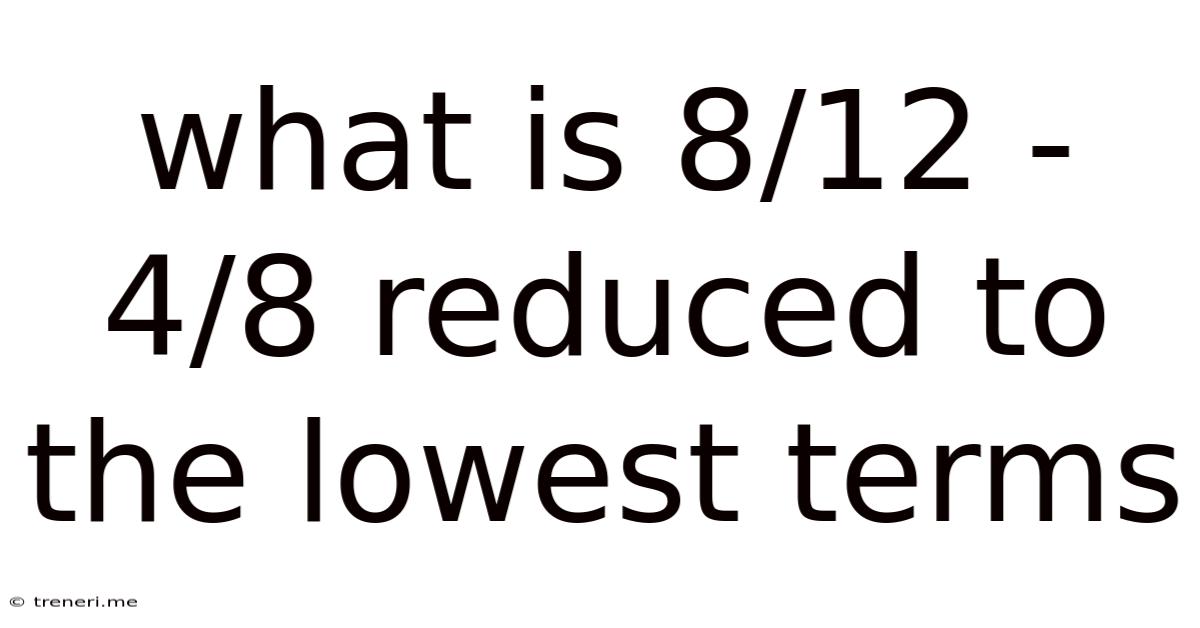
Table of Contents
What is 8/12 - 4/8 Reduced to the Lowest Terms? A Deep Dive into Fraction Simplification
Understanding fractions and simplifying them to their lowest terms is a fundamental concept in mathematics. This article will comprehensively explore the process of solving the equation 8/12 - 4/8 and reducing the result to its simplest form. We'll delve into the core principles of fraction subtraction, finding the least common denominator (LCD), and simplifying fractions using the greatest common divisor (GCD). Beyond the immediate problem, we'll also cover broader applications and strategies for working with fractions efficiently.
Understanding Fractions: A Quick Recap
Before we tackle the subtraction problem, let's review the basics of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
Step-by-Step Solution: 8/12 - 4/8
Now, let's address the problem: 8/12 - 4/8. The process involves two main steps: finding a common denominator and then performing the subtraction.
1. Finding the Least Common Denominator (LCD)
Subtracting fractions requires them to have the same denominator. To find the LCD of 12 and 8, we need to identify the smallest number that is a multiple of both. One way to do this is by listing the multiples of each number:
- Multiples of 12: 12, 24, 36, 48, 60...
- Multiples of 8: 8, 16, 24, 32, 40...
The smallest number that appears in both lists is 24. Therefore, the LCD of 12 and 8 is 24.
Alternatively, we can use the prime factorization method:
- 12 = 2 x 2 x 3
- 8 = 2 x 2 x 2
To find the LCD, we take the highest power of each prime factor present in either factorization: 2³ x 3 = 24
2. Converting Fractions to the Common Denominator
Next, we convert both fractions to have a denominator of 24:
-
8/12: To get a denominator of 24, we multiply both the numerator and denominator by 2 (since 12 x 2 = 24): (8 x 2) / (12 x 2) = 16/24
-
4/8: To get a denominator of 24, we multiply both the numerator and denominator by 3 (since 8 x 3 = 24): (4 x 3) / (8 x 3) = 12/24
3. Performing the Subtraction
Now that both fractions have the same denominator, we can subtract the numerators:
16/24 - 12/24 = (16 - 12) / 24 = 4/24
4. Reducing to Lowest Terms
The fraction 4/24 is not in its simplest form. To reduce it to its lowest terms, we need to find the greatest common divisor (GCD) of the numerator (4) and the denominator (24). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
We can find the GCD using prime factorization:
- 4 = 2 x 2
- 24 = 2 x 2 x 2 x 3
The common prime factors are 2 x 2 = 4. Therefore, the GCD of 4 and 24 is 4.
Now, we divide both the numerator and the denominator by the GCD:
4/24 = (4 ÷ 4) / (24 ÷ 4) = 1/6
Therefore, 8/12 - 4/8 reduced to its lowest terms is 1/6.
Beyond the Basics: Advanced Fraction Concepts and Applications
The problem 8/12 - 4/8 provides a springboard for understanding more advanced concepts related to fractions:
1. Finding the Greatest Common Divisor (GCD) - Alternative Methods
While prime factorization is a reliable method, other techniques exist for finding the GCD:
-
Euclidean Algorithm: This iterative algorithm is highly efficient for finding the GCD of larger numbers.
-
Listing Factors: Listing all the factors of both numbers and identifying the largest common factor. This is less efficient for large numbers but useful for smaller ones.
2. Improper Fractions and Mixed Numbers
Sometimes, the result of a fraction operation might be an improper fraction (where the numerator is larger than or equal to the denominator). For instance, if the problem yielded 7/4, this is an improper fraction. It can be converted into a mixed number (a whole number and a fraction) as follows: 7/4 = 1 and 3/4.
3. Fraction Multiplication and Division
While this problem focused on subtraction, remember that fractions can also be multiplied and divided. These operations have their own set of rules:
-
Multiplication: Multiply the numerators together and the denominators together. Simplify the resulting fraction to its lowest terms.
-
Division: Invert the second fraction (reciprocal) and then multiply.
4. Applications of Fractions in Real Life
Fractions are integral to numerous real-world applications:
-
Cooking and Baking: Recipes frequently use fractional measurements.
-
Construction and Engineering: Precise measurements and calculations require fractions.
-
Finance: Understanding percentages and interest rates involves fractions.
-
Data Analysis: Representing proportions and parts of a whole often uses fractions.
5. Using Calculators for Fraction Operations
Many calculators have built-in functions for handling fractions, simplifying them, and performing calculations. This can be a valuable tool for verifying answers and speeding up calculations, especially with more complex problems. However, understanding the underlying principles remains crucial for problem-solving and avoiding dependence solely on technology.
Conclusion: Mastering Fractions for Mathematical Proficiency
Mastering fraction operations, including simplification to lowest terms, is essential for mathematical proficiency. The seemingly simple equation 8/12 - 4/8 offers a gateway to understanding broader concepts like finding the LCD and GCD, converting between improper fractions and mixed numbers, and applying fractions in real-world scenarios. By consistently practicing these techniques and exploring different approaches, you will develop a strong foundation in fraction manipulation and improve your overall mathematical abilities. Remember that the key to success lies in understanding the underlying principles and applying them strategically, whether using manual calculations or employing calculator assistance.
Latest Posts
Latest Posts
-
What Is The Gcf Of 22 And 33
May 13, 2025
-
6 August To Today How Many Days
May 13, 2025
-
615 Rounded To The Nearest Ten
May 13, 2025
-
What Is A 4 Out Of 5 Grade
May 13, 2025
-
How Much Hours Until 6 Am
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/12 - 4/8 Reduced To The Lowest Terms . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.