What Is The Gcf Of 22 And 33
Treneri
May 13, 2025 · 5 min read
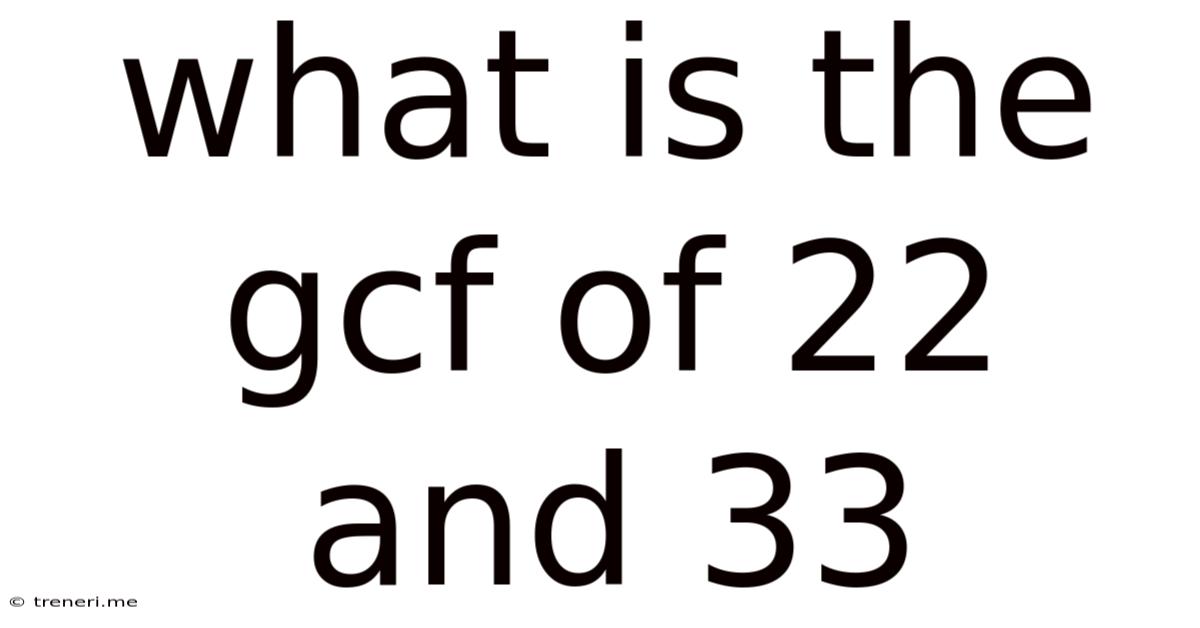
Table of Contents
What is the GCF of 22 and 33? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens up a world of mathematical understanding, useful in various applications beyond basic arithmetic. This comprehensive guide will not only answer the question "What is the GCF of 22 and 33?" but will also explore the broader context of GCFs, providing you with the tools and knowledge to tackle similar problems with confidence.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding GCFs is crucial in various mathematical operations, including simplifying fractions, solving algebraic equations, and even in more advanced areas like number theory.
Think of it like finding the biggest common building block of two numbers. For instance, if you have two piles of objects – one with 22 items and another with 33 items – the GCF would represent the largest number of items you could use to divide both piles into equal smaller groups, with nothing left over.
Methods for Finding the GCF
Several methods exist for determining the GCF of two numbers. Let's explore the most common approaches, illustrating each with examples to enhance understanding.
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 22: 1, 2, 11, 22
- Factors of 33: 1, 3, 11, 33
Comparing the lists, we see that the common factors are 1 and 11. The greatest of these is 11. Therefore, the GCF of 22 and 33 is 11.
This method is straightforward for smaller numbers but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method leverages the prime factorization of each number. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. The prime factorization of a number is the expression of that number as a product of its prime factors.
- Prime factorization of 22: 2 x 11
- Prime factorization of 33: 3 x 11
The common prime factor is 11. Therefore, the GCF of 22 and 33 is 11.
This method is particularly useful for larger numbers as it systematically breaks them down into their fundamental prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 22 and 33:
- 33 - 22 = 11
- Now we find the GCF of 22 and 11.
- 22 - 11 = 11
- The GCF is 11 because 11 and 11 are equal.
The Euclidean algorithm is significantly more efficient than listing factors, especially when dealing with large numbers. It's a foundational algorithm in number theory and computer science.
Applications of GCF
Understanding and calculating GCFs extends beyond simple arithmetic exercises. They are essential tools in various mathematical and practical applications:
1. Simplifying Fractions
GCFs play a vital role in simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF.
For example, to simplify the fraction 22/33, we find the GCF of 22 and 33, which is 11. Dividing both the numerator and the denominator by 11 gives us the simplified fraction 2/3.
2. Solving Algebraic Equations
GCFs are used in factoring algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows for simplification and further manipulation of the equation.
3. Real-World Applications
GCFs have practical applications in various fields:
- Measurement and Division: When dividing objects or measuring lengths, GCFs help determine the largest equal units for division or measurement.
- Geometry: GCFs can be utilized in geometry problems related to finding the dimensions of shapes with common factors.
- Scheduling and Time Management: GCFs can assist in determining the optimal intervals for recurring events or schedules.
Expanding on GCF Concepts
Beyond the basic calculation, let's explore some more advanced concepts related to GCFs:
Relatively Prime Numbers
Two integers are relatively prime (or coprime) if their greatest common factor is 1. For example, 22 and 27 are relatively prime because their GCF is 1. Understanding relatively prime numbers is important in number theory and cryptography.
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is divisible by both numbers. The GCF and LCM are related by the following formula:
LCM(a, b) * GCF(a, b) = a * b
Knowing the GCF allows for a quicker calculation of the LCM. The LCM is essential in solving problems involving fractions, cycles, and various practical applications.
Extended Euclidean Algorithm
The extended Euclidean algorithm is a variation of the Euclidean algorithm that not only finds the GCF of two numbers but also finds integers x and y such that:
ax + by = GCF(a, b)
This extended version is crucial in cryptography and modular arithmetic.
Conclusion: Mastering GCFs
This comprehensive exploration demonstrates that finding the GCF of 22 and 33 is merely the tip of the iceberg when it comes to understanding the concept of greatest common factors. We've delved into multiple methods for calculating the GCF, explored its various applications in mathematics and real-world scenarios, and touched upon more advanced related concepts like relatively prime numbers, LCM, and the extended Euclidean algorithm. By mastering GCFs and their related concepts, you equip yourself with a powerful set of tools for tackling a wide array of mathematical challenges and real-world problems. The seemingly simple question of "What is the GCF of 22 and 33?" ultimately opens doors to a deeper appreciation of number theory and its profound applications. Remember, the key to success lies not just in finding the answer, but in understanding the underlying principles and their wider implications.
Latest Posts
Latest Posts
-
Calculating Dg From Dh And Ds
May 13, 2025
-
Cuanto Son 9 Kilos En Libras
May 13, 2025
-
Convert Mg L To Mg Dl
May 13, 2025
-
How Many Gallons Is 71 Quarts
May 13, 2025
-
How Many Cups In 29 Ounces
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 22 And 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.