What Is The Gcf Of 32 And 24
Treneri
May 11, 2025 · 4 min read
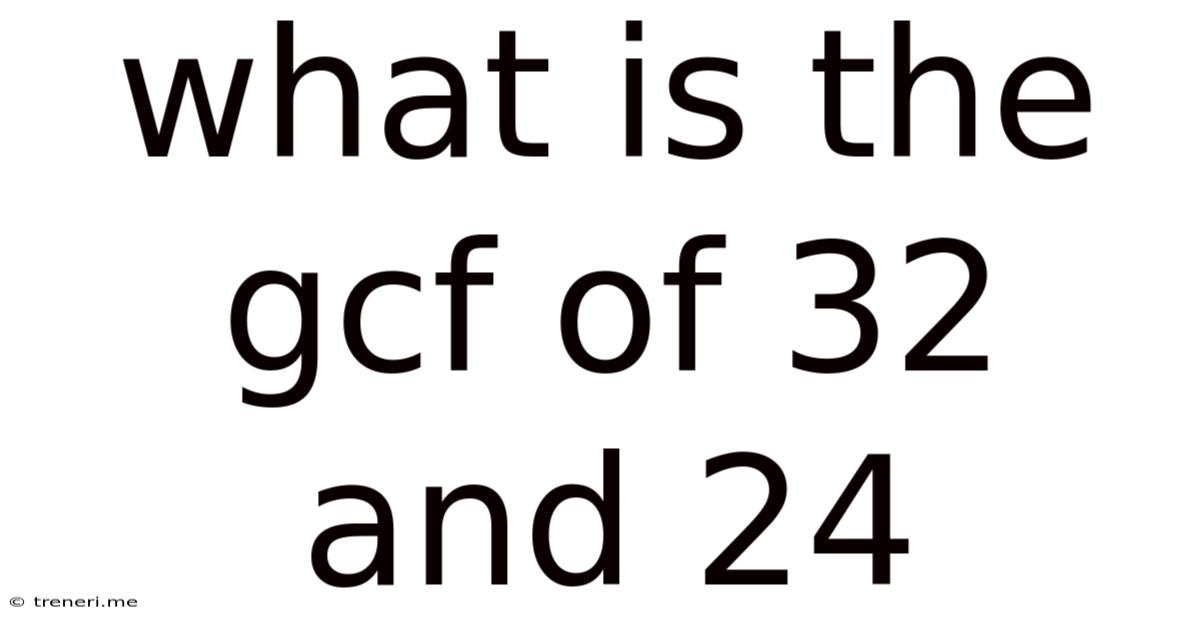
Table of Contents
What is the GCF of 32 and 24? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and various methods for solving it unlocks a deeper appreciation of number theory and its practical applications. This article will delve into the GCF of 32 and 24, exploring multiple approaches, and highlighting the significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides both numbers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between different numbers.
Why are GCFs Important?
GCFs have far-reaching applications beyond basic arithmetic. They're crucial in:
-
Simplifying Fractions: Reducing a fraction to its simplest form involves dividing both the numerator and denominator by their GCF. For instance, the fraction 24/32 can be simplified using the GCF we'll calculate.
-
Algebraic Simplification: GCFs are essential when factoring algebraic expressions. Finding the GCF of the terms allows for simplification and easier manipulation of equations.
-
Geometry and Measurement: GCFs are used in problems related to area, volume, and dividing objects into equal parts.
-
Computer Science: The concept of GCF is used in algorithms related to cryptography and number theory.
Methods for Finding the GCF of 32 and 24
Several methods exist for calculating the greatest common factor. Let's explore three common approaches:
1. Listing Factors Method
This is a straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 32: 1, 2, 4, 8, 16, 32 Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Comparing the two lists, we see that the common factors are 1, 2, 4, and 8. The greatest common factor is 8.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup> Prime factorization of 24: 2 x 2 x 2 x 3 = 2<sup>3</sup> x 3
The common prime factor is 2, and the lowest power is 2<sup>3</sup>. Therefore, the GCF is 2<sup>3</sup> = 8.
3. Euclidean Algorithm Method
This is a more efficient method for larger numbers. The Euclidean algorithm involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
- Divide the larger number (32) by the smaller number (24): 32 ÷ 24 = 1 with a remainder of 8.
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (8): 24 ÷ 8 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 8.
The Significance of the GCF of 32 and 24
Now that we've established that the GCF of 32 and 24 is 8, let's explore its significance:
-
Fraction Simplification: The fraction 24/32 can be simplified by dividing both the numerator and denominator by their GCF (8): 24/32 = (24 ÷ 8) / (32 ÷ 8) = 3/4. This simplified fraction is easier to work with and understand.
-
Problem Solving: Imagine you have 32 red marbles and 24 blue marbles. You want to divide them into identical groups with the same number of red and blue marbles in each group. The GCF (8) tells you that you can create 8 identical groups, each containing 4 red marbles and 3 blue marbles.
-
Understanding Number Relationships: The GCF reveals a fundamental relationship between two numbers. It highlights their shared divisibility properties.
Beyond the Basics: Extending the Concept
The concept of GCF extends beyond just two numbers. We can find the GCF of multiple numbers using similar methods. For instance, to find the GCF of 32, 24, and 16, we could use prime factorization or the Euclidean algorithm (modified for multiple numbers).
Conclusion: The Power of the GCF
Finding the GCF, whether for 32 and 24 or larger numbers, is more than just a mathematical exercise. It's a fundamental concept that underpins various aspects of mathematics, problem-solving, and even computer science. Understanding the different methods for finding the GCF equips you with valuable tools for simplifying problems and gaining deeper insights into number relationships. The seemingly simple task of finding the GCF of 32 and 24 unveils the elegance and power of fundamental mathematical principles. Mastering this concept opens doors to a deeper understanding of more complex mathematical ideas and their applications in the real world. From simplifying fractions to solving complex equations, the GCF is a cornerstone of numerical analysis and provides a powerful framework for various problem-solving approaches. Therefore, understanding and applying the GCF concept remains a valuable skill for students, mathematicians, and anyone working with numbers.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 5 And 10
May 12, 2025
-
What Is 30 Of 1 Million
May 12, 2025
-
Gcf Of 7 15 And 21
May 12, 2025
-
75 Grams Of Butter In Tablespoons
May 12, 2025
-
What Is 100 Percent Of 100
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 32 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.