What Is The Gcf Of 32 And 54
Treneri
May 09, 2025 · 5 min read
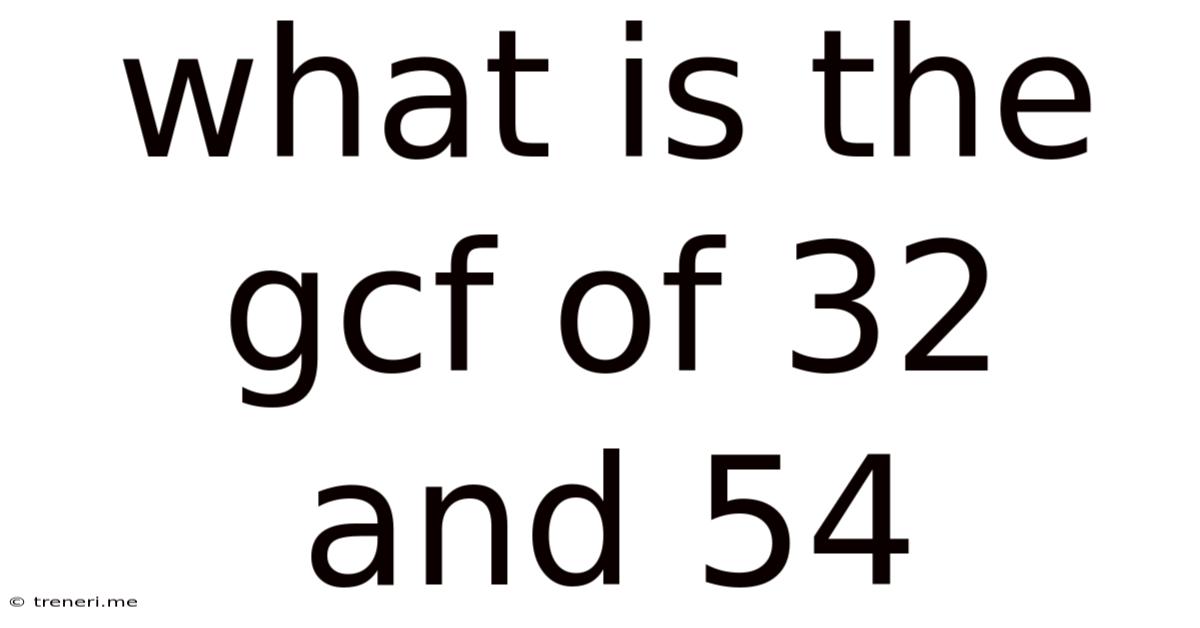
Table of Contents
What is the GCF of 32 and 54? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods involved can be surprisingly enriching. This article will explore the GCF of 32 and 54 in detail, examining various approaches and highlighting the broader significance of GCF in mathematics and beyond. We'll go beyond a simple answer and delve into the 'why' and 'how' to solidify your understanding.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. This concept is fundamental in various mathematical operations, including simplifying fractions, solving equations, and understanding number theory.
Think of it like finding the largest common building block of two numbers. If you have 32 apples and 54 oranges, and you want to divide them into the largest possible equal groups without any leftovers, the GCF will tell you how many items can be in each group.
Method 1: Prime Factorization
This method is considered a classic and reliable way to find the GCF. It involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 32
32 can be broken down as follows:
- 32 = 2 x 16
- 16 = 2 x 8
- 8 = 2 x 4
- 4 = 2 x 2
Therefore, the prime factorization of 32 is 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
Step 2: Prime Factorization of 54
54 can be broken down as follows:
- 54 = 2 x 27
- 27 = 3 x 9
- 9 = 3 x 3
Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3 = 2 x 3<sup>3</sup>
Step 3: Identifying Common Factors
Now, compare the prime factorizations of 32 and 54:
32 = 2<sup>5</sup> 54 = 2 x 3<sup>3</sup>
The only common prime factor is 2. It appears once in the factorization of 54 and five times in the factorization of 32. We take the lowest power of the common factor.
Step 4: Calculating the GCF
The GCF is the product of the common prime factors raised to their lowest power. In this case, the only common prime factor is 2, and its lowest power is 2<sup>1</sup> = 2.
Therefore, the GCF of 32 and 54 is $\boxed{2}$.
Method 2: Listing Factors
This method is simpler for smaller numbers but can become cumbersome for larger ones.
Step 1: List the Factors of 32
The factors of 32 are: 1, 2, 4, 8, 16, 32
Step 2: List the Factors of 54
The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54
Step 3: Identify Common Factors
Compare the two lists and find the common factors: 1 and 2
Step 4: Determine the Greatest Common Factor
The greatest common factor among these common factors is 2.
Therefore, the GCF of 32 and 54 is $\boxed{2}$.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Step 1: Repeated Subtraction (or Division with Remainder)
Let's start with 54 and 32.
- 54 - 32 = 22
- 32 - 22 = 10
- 22 - 10 = 12
- 12 - 10 = 2
- 10 - 2 = 8
- 8 - 2 = 6
- 6 - 2 = 4
- 4 - 2 = 2
- 2 - 2 = 0
The last non-zero remainder is 2.
Alternatively, using the division method:
- 54 ÷ 32 = 1 with a remainder of 22
- 32 ÷ 22 = 1 with a remainder of 10
- 22 ÷ 10 = 2 with a remainder of 2
- 10 ÷ 2 = 5 with a remainder of 0
The last non-zero remainder is 2.
Step 2: The GCF
The last non-zero remainder is the GCF. Therefore, the GCF of 32 and 54 is $\boxed{2}$.
Applications of GCF
The concept of GCF extends far beyond simple arithmetic problems. It has significant applications in various fields:
-
Simplifying Fractions: To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, the fraction 32/54 can be simplified to 16/27 by dividing both by their GCF, 2.
-
Solving Diophantine Equations: GCF plays a crucial role in solving Diophantine equations, which are algebraic equations where only integer solutions are sought.
-
Modular Arithmetic: GCF is essential in understanding modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
-
Geometry: GCF is used in finding the dimensions of the largest square that can perfectly tile a given rectangle.
Conclusion: Beyond the Numbers
While finding the GCF of 32 and 54 might seem like a straightforward calculation, exploring the different methods highlights the richness and interconnectedness of mathematical concepts. Understanding these methods not only provides you with the answer but also develops critical thinking skills and a deeper appreciation for the elegance of mathematics. Remember, the choice of method depends on the context and the size of the numbers involved. For smaller numbers, listing factors might be sufficient, while for larger numbers, the Euclidean algorithm offers a more efficient approach. The prime factorization method, however, offers a fundamental understanding of the structure of numbers themselves. Mastering these techniques equips you with valuable tools applicable in various mathematical areas and beyond.
Latest Posts
Latest Posts
-
How Many Days Since September 7th
May 09, 2025
-
5 11 At 16 How Tall Will I Be
May 09, 2025
-
27 Gallons Equals How Many Quarts
May 09, 2025
-
15 Is 25 Percent Of What Number
May 09, 2025
-
How Long Have You Been Married Calculator
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 32 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.