What Is The Gcf Of 32 And 80
Treneri
May 11, 2025 · 6 min read
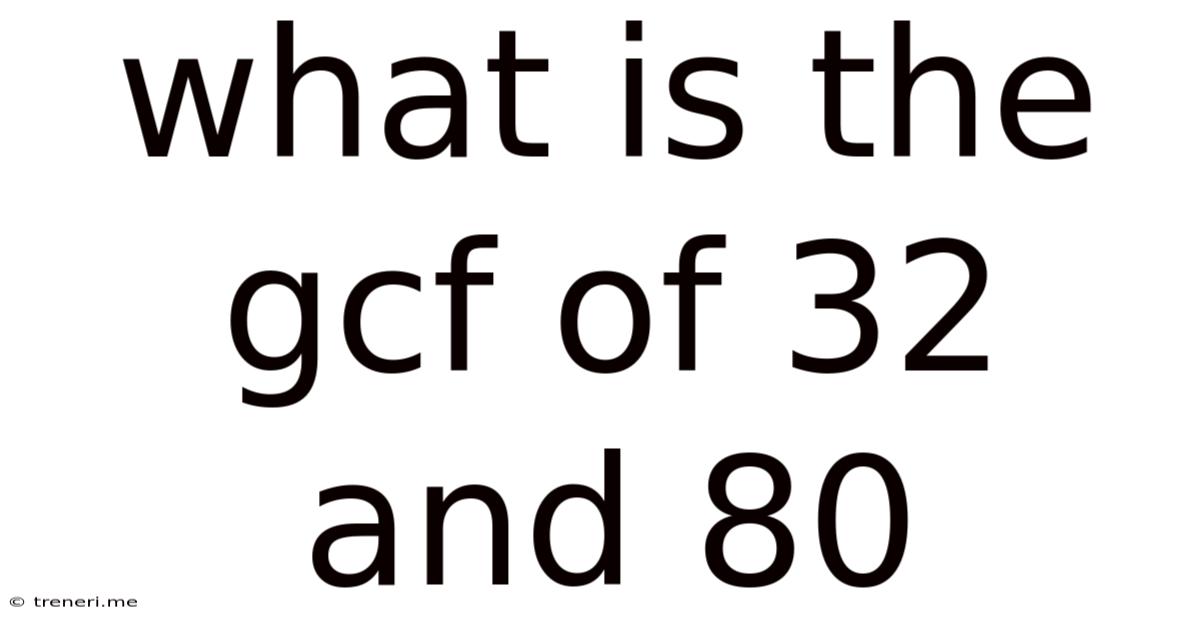
Table of Contents
What is the GCF of 32 and 80? A Comprehensive Guide to Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will delve into the methods of determining the GCF of 32 and 80, exploring different approaches and providing a thorough understanding of the underlying principles. We'll also examine the broader context of GCFs and their importance in mathematics.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as greatestcommon divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Why is Finding the GCF Important?
Determining the GCF is crucial for various mathematical operations and real-world applications:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms. For instance, simplifying 12/18 requires finding the GCF (which is 6), resulting in the simplified fraction 2/3.
-
Solving Equations: GCF plays a vital role in solving algebraic equations, particularly when factoring polynomials.
-
Geometry and Measurement: GCF is used in geometry problems involving finding the dimensions of shapes or determining the largest possible square tile to cover a rectangular area.
-
Real-world Applications: GCF finds application in various real-world scenarios, such as dividing items equally among groups, determining the largest common unit for measurements, and in computer programming for optimizing algorithms.
Methods for Finding the GCF of 32 and 80
Several methods can be used to determine the GCF of 32 and 80. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and identifying the largest common factor.
Factors of 32: 1, 2, 4, 8, 16, 32
Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Comparing the two lists, we identify the common factors: 1, 2, 4, 8, 16. The greatest of these common factors is 16. Therefore, the GCF of 32 and 80 is 16.
This method is straightforward for smaller numbers but becomes cumbersome for larger numbers with numerous factors.
2. Prime Factorization
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 32:
32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
Prime Factorization of 80:
80 = 2 x 40 = 2 x 2 x 20 = 2 x 2 x 2 x 10 = 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
The common prime factor is 2, and the lowest power of 2 present in both factorizations is 2<sup>4</sup> (which equals 16). Therefore, the GCF of 32 and 80 is 16.
Prime factorization is a more efficient method for larger numbers, especially when dealing with multiple numbers.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes tedious. The algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply the Euclidean algorithm to find the GCF of 32 and 80:
-
Start with the larger number (80) and the smaller number (32).
-
Divide the larger number by the smaller number and find the remainder.
80 ÷ 32 = 2 with a remainder of 16
-
Replace the larger number with the smaller number and the smaller number with the remainder.
Now we have the numbers 32 and 16.
-
Repeat the process:
32 ÷ 16 = 2 with a remainder of 0
-
When the remainder is 0, the GCF is the last non-zero remainder.
In this case, the last non-zero remainder is 16. Therefore, the GCF of 32 and 80 is 16.
The Euclidean algorithm is highly efficient and is often used in computer programs to calculate GCFs of very large numbers.
GCF in Different Contexts
The concept of GCF extends beyond simple number pairs. Let's explore its application in various mathematical domains:
GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 32, 80, and 48:
-
Prime Factorization:
- 32 = 2<sup>5</sup>
- 80 = 2<sup>4</sup> x 5
- 48 = 2<sup>4</sup> x 3
The common prime factor is 2, and the lowest power is 2<sup>4</sup> = 16. Therefore, the GCF(32, 80, 48) = 16.
-
Euclidean Algorithm (extended): The Euclidean algorithm can be extended to handle multiple numbers by repeatedly finding the GCF of pairs of numbers. First, find the GCF of two numbers, then find the GCF of the result and the third number, and so on.
GCF and Least Common Multiple (LCM)
The GCF and LCM (least common multiple) are closely related. The product of the GCF and LCM of two numbers is equal to the product of the two numbers. This relationship is useful in various mathematical problems.
For 32 and 80:
- GCF(32, 80) = 16
- LCM(32, 80) = 160
Notice that 16 x 160 = 2560, and 32 x 80 = 2560. This verifies the relationship between GCF and LCM.
Conclusion: Mastering the GCF
Understanding the concept of the greatest common factor and mastering the various methods for calculating it is essential for a strong foundation in mathematics. Whether using the listing factors method, prime factorization, or the efficient Euclidean algorithm, the choice of method depends on the complexity of the numbers involved. This comprehensive guide has provided a thorough exploration of finding the GCF, particularly for the numbers 32 and 80, highlighting its importance in various mathematical contexts and real-world applications. With a firm grasp of these concepts, you'll be well-equipped to tackle more advanced mathematical problems and appreciate the power of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Is 24 Out Of 40 As A Percentage
May 12, 2025
-
Can You Tan With 3 Uv
May 12, 2025
-
How Many Days Since August 31st
May 12, 2025
-
How To Calculate Kva To Amps
May 12, 2025
-
Comment Calculer La Hauteur D Un Cylindre
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 32 And 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.