What Is The Gcf Of 4 And 18
Treneri
May 14, 2025 · 5 min read
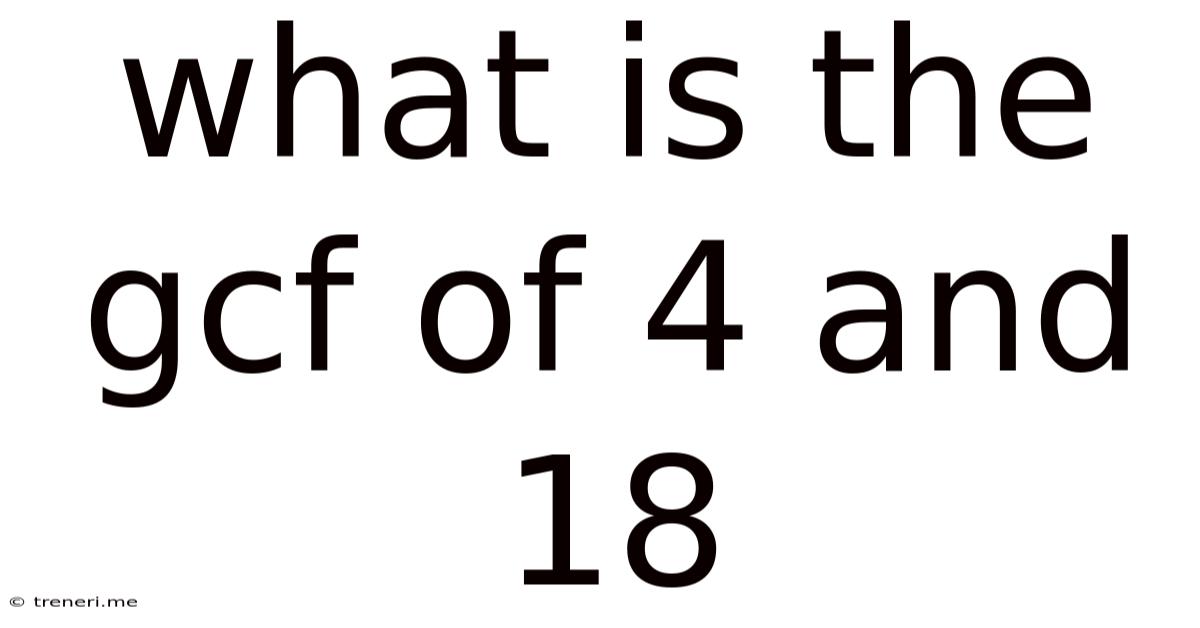
Table of Contents
What is the GCF of 4 and 18? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it opens up a world of mathematical understanding. This article will delve deep into determining the GCF of 4 and 18, exploring multiple approaches, and expanding on the broader significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor, also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and various other mathematical applications.
Why are GCFs Important?
GCFs aren't just abstract mathematical concepts; they have practical applications in various fields:
- Simplifying Fractions: Finding the GCF allows us to reduce fractions to their simplest form. For example, the fraction 18/4 can be simplified using the GCF of 18 and 4.
- Algebraic Simplification: GCFs play a crucial role in factoring algebraic expressions, making them easier to manipulate and solve.
- Geometry and Measurement: GCFs are used in solving geometric problems involving area, perimeter, and volume, often by finding the dimensions of the largest possible square or cube that can fit within a given shape.
- Real-World Applications: GCFs are applied in situations involving dividing quantities into equal groups, such as distributing items evenly or arranging objects in arrays.
Finding the GCF of 4 and 18: Multiple Methods
Let's explore different methods to find the GCF of 4 and 18:
Method 1: Listing Factors
This is a straightforward method, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 4: 1, 2, 4 Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1 and 2. The greatest of these common factors is 2. Therefore, the GCF of 4 and 18 is 2.
Method 2: Prime Factorization
This method involves expressing each number as a product of its prime factors. The prime factors are the building blocks of numbers, only divisible by 1 and themselves.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
Now, we identify the common prime factors and multiply them to find the GCF. Both 4 and 18 share one factor of 2. Therefore, the GCF is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on repeatedly applying the division algorithm.
- Divide the larger number (18) by the smaller number (4): 18 ÷ 4 = 4 with a remainder of 2.
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (2): Now we find the GCF of 4 and 2.
- Divide 4 by 2: 4 ÷ 2 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 2.
Therefore, the GCF of 4 and 18 is 2.
Expanding on the Concept of GCF
Understanding the GCF goes beyond simply finding the answer for specific numbers. It's a cornerstone of number theory and has far-reaching implications.
GCF and LCM: A Complementary Relationship
The greatest common factor (GCF) and the least common multiple (LCM) are intimately related. The LCM is the smallest number that is a multiple of both numbers. For 4 and 18:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36...
- Multiples of 18: 18, 36, 54...
The smallest number appearing in both lists is 36. Therefore, the LCM of 4 and 18 is 36.
There's a crucial relationship between the GCF and LCM of two numbers (a and b):
a x b = GCF(a, b) x LCM(a, b)
In our case: 4 x 18 = 72, and 2 x 36 = 72. This relationship holds true for any two positive integers.
Applications in Abstract Algebra
The concept of GCF extends far beyond elementary arithmetic. In abstract algebra, the GCF finds applications in ring theory and ideal theory, where the focus shifts from integers to more abstract algebraic structures.
GCF in Computer Science
The Euclidean algorithm, used to find the GCF, is a fundamental algorithm in computer science. Its efficiency and elegance make it a key component in various cryptographic systems and other computational tasks.
Advanced Techniques for Finding GCF
While the methods described earlier are suitable for smaller numbers, more advanced techniques exist for handling larger numbers or situations requiring significant computational efficiency.
Using a Calculator or Software
Most scientific calculators and mathematical software packages (like Mathematica, MATLAB, or Python libraries) have built-in functions for calculating the GCF. These tools are particularly helpful when dealing with large numbers.
The Extended Euclidean Algorithm
The extended Euclidean algorithm not only finds the GCF but also provides integers x and y such that:
ax + by = GCF(a, b)
This extended version has applications in cryptography and solving linear Diophantine equations.
Conclusion
Finding the GCF of 4 and 18, as demonstrated above, reveals much more than just a simple answer (2). It illuminates fundamental mathematical concepts, unveils connections between seemingly disparate areas of mathematics, and showcases the practicality of these concepts in various applications. From simplifying fractions to sophisticated cryptographic systems, the GCF plays a crucial role in mathematics and beyond, highlighting the enduring power of seemingly simple arithmetic principles. Mastering the various methods for calculating the GCF equips you with a powerful tool for tackling diverse mathematical challenges.
Latest Posts
Latest Posts
-
How Much Is 5 Quarts Of Popcorn
May 14, 2025
-
What Is The Greatest Common Factor Of 42 And 24
May 14, 2025
-
How To Find The Height Of Trapezoid
May 14, 2025
-
20 Divided By 3 With Remainder
May 14, 2025
-
90 Days From Oct 22 2024
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 4 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.