What Is The Gcf Of 8 And 18
Treneri
May 12, 2025 · 5 min read
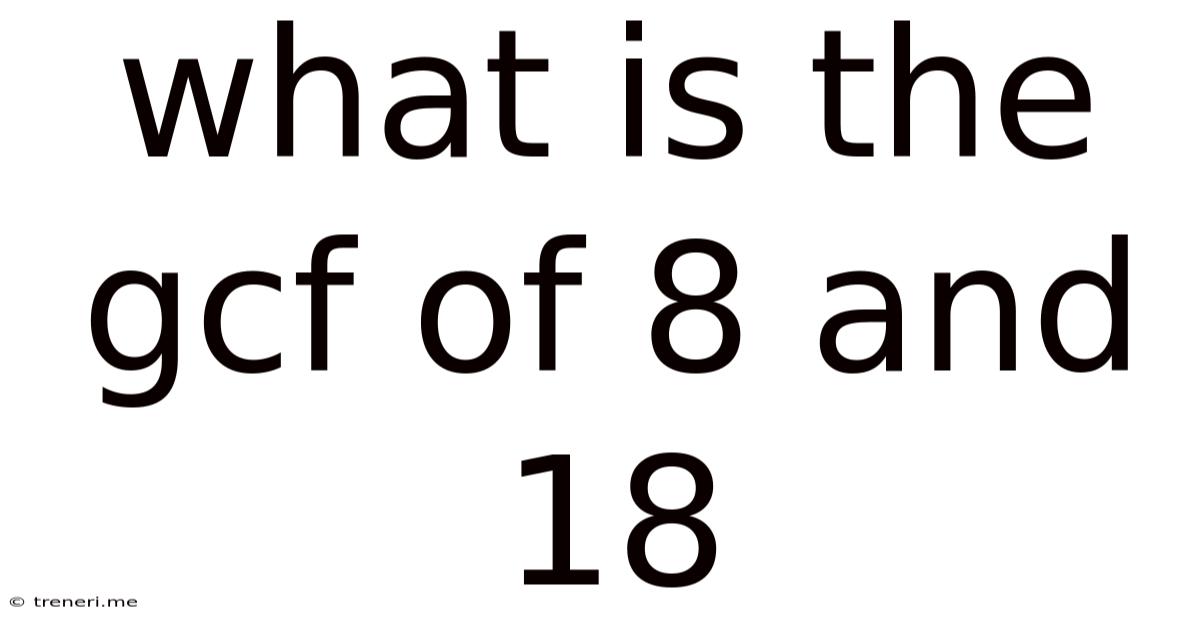
Table of Contents
What is the GCF of 8 and 18? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods can significantly enhance your mathematical skills and problem-solving abilities. This article explores the GCF of 8 and 18 in detail, delving into multiple approaches, practical applications, and the broader significance of this fundamental concept in mathematics.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a cornerstone of number theory and has wide-ranging applications in various fields, from simplifying fractions to solving complex algebraic equations.
In simpler terms, the GCF represents the biggest number that can be found in both numbers without leaving anything left over. Think of it as the largest common "building block" of those numbers.
Methods for Finding the GCF of 8 and 18
Several methods can be employed to determine the GCF of 8 and 18. Let's explore three common approaches:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 8: 1, 2, 4, 8
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the two lists, we see that the common factors are 1 and 2. The greatest common factor is therefore 2.
2. Prime Factorization
This method leverages the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
To find the GCF using prime factorization, we identify the common prime factors and multiply them together. In this case, both 8 and 18 share only one 2. Therefore, the GCF is 2.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply the Euclidean algorithm to 8 and 18:
- 18 - 8 = 10 (Now we find the GCF of 8 and 10)
- 10 - 8 = 2 (Now we find the GCF of 8 and 2)
- 8 - 2 - 2 - 2 - 2 = 0 (The GCF is the last non-zero remainder; hence it is 2)
Therefore, the GCF of 8 and 18, using the Euclidean algorithm, is 2.
Applications of Finding the GCF
The ability to find the GCF is not just an academic exercise; it has practical applications across various mathematical domains and real-world scenarios:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 18/8 can be simplified by dividing both the numerator and the denominator by their GCF (2), resulting in the simplified fraction 9/4.
-
Solving Equations: GCF plays a vital role in solving certain types of equations, particularly those involving polynomial expressions. Factoring out the GCF helps simplify and solve these equations more efficiently.
-
Measurement and Geometry: GCF is essential when dealing with problems involving measurement and geometric shapes. For instance, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the floor's length and width.
-
Modular Arithmetic: The concept of GCF underpins many aspects of modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Data Analysis: In data analysis, finding the common factors between datasets can reveal underlying relationships and patterns. Identifying the GCF in such scenarios can lead to more effective data interpretation.
Further Exploration of Number Theory Concepts Related to GCF
Understanding the GCF opens doors to further exploration of related number theory concepts:
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more numbers. The GCF and LCM are intimately related; their product is equal to the product of the original two numbers (GCF x LCM = Number1 x Number2). This relationship provides a shortcut for finding the LCM once the GCF is known.
-
Prime Numbers: Prime numbers are the building blocks of all other numbers. Understanding prime factorization is fundamental to efficiently finding the GCF.
-
Divisibility Rules: Knowing divisibility rules (rules to quickly determine if a number is divisible by another) can streamline the process of finding factors and, consequently, the GCF.
-
Euclidean Algorithm Efficiency: The Euclidean algorithm is particularly efficient because its computational complexity is logarithmic, meaning the number of steps required increases slowly with the size of the numbers involved.
Conclusion: The Significance of the GCF
The seemingly simple task of finding the GCF of 8 and 18 – which we've determined to be 2 – unveils a wealth of mathematical concepts and practical applications. Mastering this concept is not just about finding the answer to a specific problem; it's about developing a deeper understanding of number theory, improving problem-solving skills, and gaining a valuable tool applicable across various mathematical and real-world contexts. The methods explored in this article – listing factors, prime factorization, and the Euclidean algorithm – offer diverse approaches, each valuable in different situations. Further exploration of related concepts such as the LCM and prime numbers will solidify your mathematical foundation and open up further avenues of learning and application. The GCF is more than just a mathematical concept; it's a fundamental building block for more advanced mathematical reasoning and problem-solving.
Latest Posts
Latest Posts
-
Como Calcular El Interes Compuesto Diario
May 14, 2025
-
10 Out Of 16 In Percentage
May 14, 2025
-
What Is 68 9 Inches In Feet
May 14, 2025
-
21 Out Of 30 Is What Percent
May 14, 2025
-
How Many Cups In 5 Pounds Of Rice
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.