What Is The Gcf Of 8 And 28
Treneri
May 12, 2025 · 5 min read
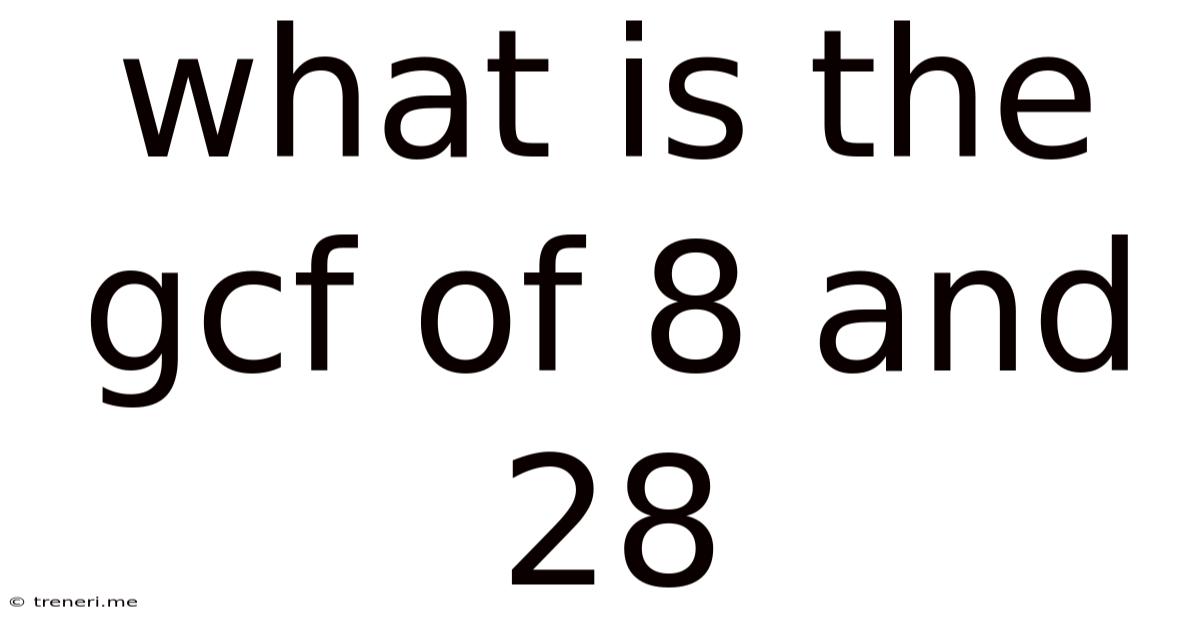
Table of Contents
What is the GCF of 8 and 28? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it opens doors to more complex mathematical concepts. This article will explore the GCF of 8 and 28 in detail, providing multiple approaches to solving the problem and expanding on the significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding GCFs is crucial in simplifying fractions, solving algebraic equations, and various other mathematical operations.
Why are GCFs Important?
GCFs are fundamental in many areas of mathematics and its applications:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to reduce a fraction to its simplest form. For example, the fraction 12/18 can be simplified by finding the GCF of 12 and 18 (which is 6), resulting in the equivalent fraction 2/3.
-
Algebraic Expressions: GCFs play a critical role in factoring algebraic expressions. Factoring allows us to simplify complex expressions and solve equations more efficiently.
-
Geometry and Measurement: GCFs are used in problems involving geometric shapes and measurements, such as finding the largest square tile that can perfectly cover a rectangular floor.
-
Number Theory: GCFs are a core concept in number theory, a branch of mathematics dealing with the properties of integers.
Methods for Finding the GCF of 8 and 28
There are several methods for determining the GCF of two numbers. Let's apply these methods to find the GCF of 8 and 28:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 28: 1, 2, 4, 7, 14, 28
The common factors of 8 and 28 are 1, 2, and 4. The greatest common factor is 4.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 28: 2 x 2 x 7 = 2² x 7
The common prime factor is 2, and the lowest power of 2 in both factorizations is 2². Therefore, the GCF is 2² = 4.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
- Divide the larger number (28) by the smaller number (8): 28 ÷ 8 = 3 with a remainder of 4.
- Replace the larger number with the remainder (4) and repeat the process: 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
GCF in Real-World Applications
The concept of GCF isn't confined to theoretical mathematics; it has practical applications in various real-world scenarios:
-
Recipe Scaling: Imagine you have a recipe that serves 8 people, but you need to scale it down to serve 4. Finding the GCF of 8 and 4 (which is 4) helps you determine the scaling factor. You would divide each ingredient quantity by 2 (8/4=2).
-
Tiling and Flooring: When tiling a floor, you want to use tiles of the largest possible size that fit perfectly. If your room dimensions are 28 feet by 8 feet, the GCF (4) represents the size of the largest square tile (4ft x 4ft) that can cover the floor without needing to cut tiles.
-
Resource Allocation: If you have 8 red marbles and 28 blue marbles, and you want to divide them into identical groups, the GCF helps you determine the maximum number of identical groups you can create. You could make 4 groups, each with 2 red marbles and 7 blue marbles.
Expanding on the Concept of GCF
Understanding GCFs provides a foundation for grasping more advanced mathematical concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the formula: GCF(a, b) * LCM(a, b) = a * b. Knowing the GCF helps in efficiently calculating the LCM.
-
Modular Arithmetic: GCFs are crucial in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus).
-
Diophantine Equations: These equations involve finding integer solutions to algebraic equations. The GCF plays a significant role in determining the existence and nature of such solutions.
Conclusion: The Power of the GCF
The seemingly simple concept of the greatest common factor has far-reaching implications in various fields, from simplifying fractions to solving complex equations. Understanding the different methods for calculating the GCF—listing factors, prime factorization, and the Euclidean algorithm—equips you with valuable tools for tackling mathematical problems efficiently. More importantly, mastering the concept of GCF helps build a strong foundation for more advanced mathematical exploration and problem-solving. Therefore, finding the GCF of 8 and 28, while seemingly straightforward, represents a gateway to a deeper understanding of numerical relationships and their practical applications. The answer, as we've demonstrated using various methods, is definitively 4.
Latest Posts
Latest Posts
-
2 Tsp Minced Garlic To Garlic Powder
May 14, 2025
-
What Is 50 Percent Of 16
May 14, 2025
-
Find All The Real Fourth Roots Of
May 14, 2025
-
How Many Ounces In 86 Grams
May 14, 2025
-
90 Days From Sep 24 2024
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.