What Is The Gcf Of 96 And 84
Treneri
May 11, 2025 · 5 min read
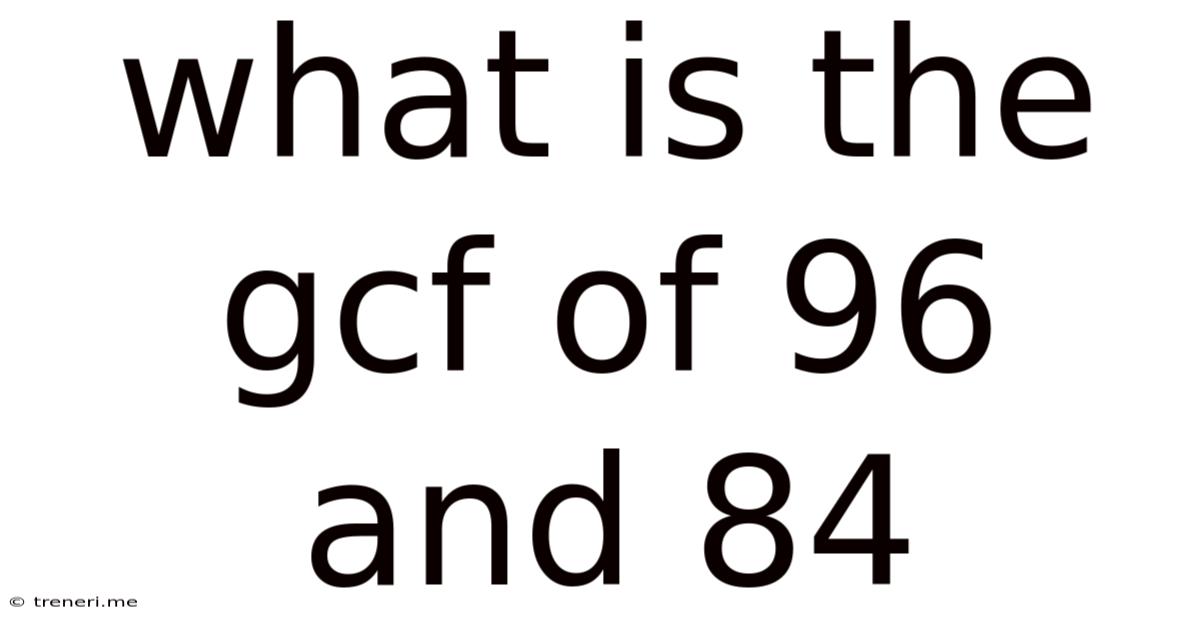
Table of Contents
What is the GCF of 96 and 84? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can be surprisingly enriching. This article will delve into determining the GCF of 96 and 84, not just by providing the answer, but by explaining the process in detail, introducing various techniques, and highlighting the broader significance of GCF in mathematics and beyond.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding GCF is crucial in various mathematical operations, including simplifying fractions, solving algebraic equations, and working with geometric problems.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
1. Prime Factorization of 96:
96 can be factored as follows:
96 = 2 x 48 = 2 x 2 x 24 = 2 x 2 x 2 x 12 = 2 x 2 x 2 x 2 x 6 = 2 x 2 x 2 x 2 x 2 x 3 = 2<sup>5</sup> x 3
2. Prime Factorization of 84:
84 can be factored as follows:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2<sup>2</sup> x 3 x 7
3. Identifying Common Factors:
Now, we compare the prime factorizations of 96 and 84:
96 = 2<sup>5</sup> x 3 84 = 2<sup>2</sup> x 3 x 7
The common factors are 2<sup>2</sup> and 3.
4. Calculating the GCF:
To find the GCF, we multiply the common prime factors raised to their lowest powers:
GCF(96, 84) = 2<sup>2</sup> x 3 = 4 x 3 = 12
Therefore, the greatest common factor of 96 and 84 is 12.
Method 2: The Euclidean Algorithm
The Euclidean algorithm provides a more efficient method, particularly for larger numbers. This iterative algorithm involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
1. Applying the Division Algorithm:
We begin by dividing the larger number (96) by the smaller number (84):
96 ÷ 84 = 1 with a remainder of 12
2. Iterating the Process:
Now, we replace the larger number with the smaller number (84) and the smaller number with the remainder (12):
84 ÷ 12 = 7 with a remainder of 0
3. Determining the GCF:
Since the remainder is 0, the last non-zero remainder (12) is the GCF.
Therefore, the GCF(96, 84) = 12.
Method 3: Listing Factors
This method is suitable for smaller numbers and involves listing all the factors of each number and identifying the largest common factor.
1. Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
2. Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
3. Identifying Common Factors:
Comparing the lists, the common factors are 1, 2, 3, 4, 6, and 12.
4. Determining the GCF:
The largest common factor is 12.
Applications of GCF in Real-World Scenarios
The concept of GCF extends far beyond the realm of abstract mathematics. It finds practical applications in various fields:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms. For example, the fraction 96/84 can be simplified to 8/7 by dividing both the numerator and denominator by their GCF, 12.
-
Geometry: GCF is used in determining the dimensions of the largest square tile that can perfectly cover a rectangular area. If you have a rectangular floor measuring 96 inches by 84 inches, the largest square tile that can fit without any cutting would have sides of 12 inches (the GCF of 96 and 84).
-
Dividing Objects: Imagine you have 96 apples and 84 oranges. You want to divide them into identical groups with the maximum number of items in each group. The GCF (12) tells you that you can create 12 groups, each containing 8 apples and 7 oranges.
-
Data Organization: In computer science, GCF can be utilized in data compression and organization algorithms.
-
Music Theory: The GCF can help in finding the greatest common divisor of musical intervals, which is crucial in music theory and harmony.
Beyond the Basics: Exploring LCM
While this article focused on GCF, it's important to mention the closely related concept of the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. GCF and LCM are interconnected; their product equals the product of the two original numbers. For 96 and 84:
GCF(96, 84) x LCM(96, 84) = 96 x 84
Since GCF(96, 84) = 12, we can calculate the LCM:
12 x LCM(96, 84) = 8064
LCM(96, 84) = 8064 ÷ 12 = 672
Conclusion: The Significance of GCF
The seemingly simple task of finding the GCF of 96 and 84 opens a window into the fascinating world of number theory. Understanding the different methods – prime factorization, the Euclidean algorithm, and listing factors – not only provides a solid foundation in arithmetic but also highlights the practical applications of this concept across various disciplines. From simplifying fractions to solving real-world problems, the GCF proves to be a versatile and essential tool in mathematics and beyond. The ability to efficiently calculate GCF, and its close relative LCM, is a fundamental skill for students and professionals alike. Mastering these concepts unlocks a deeper understanding of numerical relationships and their practical significance.
Latest Posts
Latest Posts
-
1 3 1 2 In Fraction Form
May 12, 2025
-
18 Is What Percentage Of 30
May 12, 2025
-
1500 Eosinophils Per Microliter In Percentage
May 12, 2025
-
Cuanto Es 200 Hectareas En Metros
May 12, 2025
-
What Is 109 Fahrenheit In Celsius
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 96 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.