What Is The Greatest Common Factor Of 28 And 72
Treneri
May 09, 2025 · 6 min read
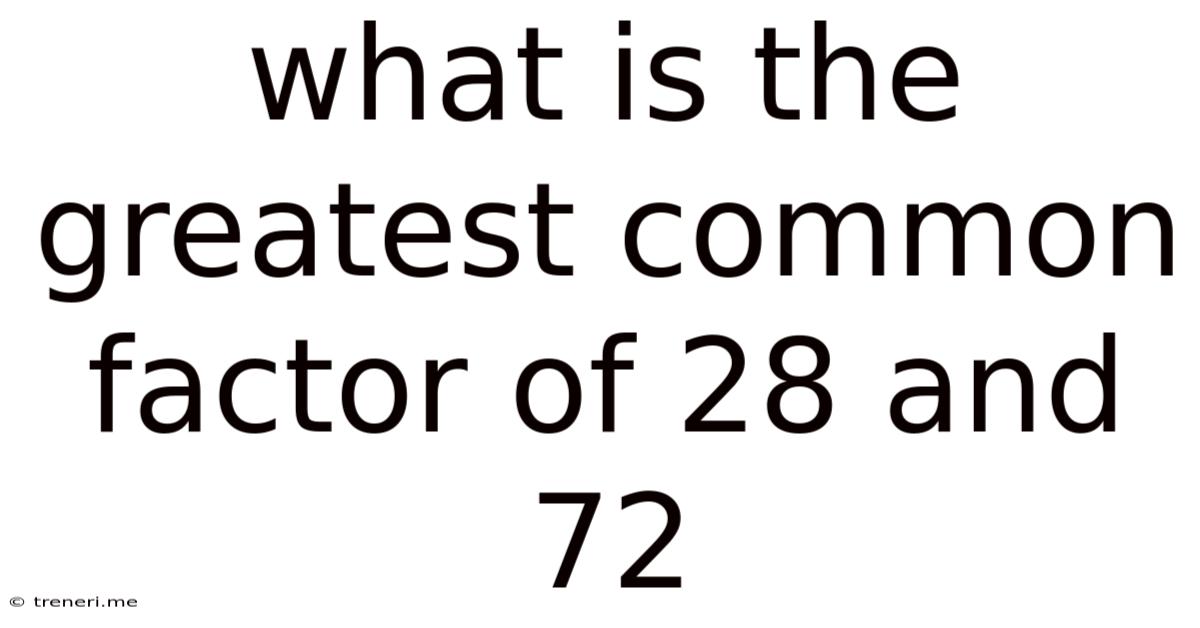
Table of Contents
What is the Greatest Common Factor of 28 and 72? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications spanning various fields, from simplifying fractions to solving complex algebraic equations. This article delves into the methods for determining the GCF of 28 and 72, exploring different approaches and highlighting the underlying mathematical principles. We'll go beyond simply finding the answer and explore the broader implications and applications of this concept.
Understanding Greatest Common Factors
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be evenly divided into both numbers. Understanding GCFs is crucial for simplifying fractions, solving Diophantine equations, and even in more advanced mathematical concepts.
Why is finding the GCF important?
The applications of finding the GCF extend beyond simple mathematical exercises. Here are some key areas where this concept proves invaluable:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For instance, if we have the fraction 28/72, finding the GCF helps us simplify it to its lowest terms.
-
Solving Equations: GCFs play a crucial role in solving various types of equations, particularly Diophantine equations (equations where only integer solutions are considered).
-
Understanding Number Relationships: Finding the GCF provides insight into the relationship between two numbers, revealing common factors and divisors.
-
Modular Arithmetic: The concept of GCF is fundamental in modular arithmetic, which has applications in cryptography and computer science.
-
Geometry and Measurement: GCFs are often used in solving geometric problems involving area, perimeter, and other measurements.
Methods for Finding the GCF of 28 and 72
Several methods can efficiently determine the GCF of 28 and 72. Let's explore some of the most common techniques:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 28: 1, 2, 4, 7, 14, 28 Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Comparing the two lists, we observe that the common factors are 1, 2, and 4. The greatest among these is 4. Therefore, the GCF of 28 and 72 is 4.
This method is straightforward for smaller numbers but can become cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 28: 2² × 7 Prime factorization of 72: 2³ × 3²
The only common prime factor is 2. The lowest power of 2 present in both factorizations is 2². Therefore, the GCF is 2² = 4.
This method is more efficient than the listing factors method, particularly for larger numbers, as it systematically breaks down the numbers into their prime constituents.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially for larger numbers where the listing factors or prime factorization methods become less practical. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to find the GCF of 28 and 72:
- 72 ÷ 28 = 2 with a remainder of 16
- 28 ÷ 16 = 1 with a remainder of 12
- 16 ÷ 12 = 1 with a remainder of 4
- 12 ÷ 4 = 3 with a remainder of 0
The last non-zero remainder is 4, which is the GCF of 28 and 72.
The Euclidean algorithm is highly efficient and avoids the need to find all factors or prime factorize large numbers. It's particularly useful in computer programming for GCF calculations.
Applications of GCF in Real-World Scenarios
The concept of GCF extends beyond abstract mathematical problems; it finds practical applications in various real-world scenarios:
-
Baking: Imagine you're baking and have 28 ounces of flour and 72 ounces of sugar. To maintain the recipe's proportions while using the smallest possible quantities, you'd divide both by their GCF (4). This would yield 7 ounces of flour and 18 ounces of sugar, maintaining the same ratio.
-
Gardening: You have 28 red tulips and 72 yellow tulips. You want to plant them in rows with an equal number of each color in each row. The GCF (4) tells you that you can plant them in 4 rows, each containing 7 red and 18 yellow tulips.
-
Construction: Suppose you need to cut tiles of 28 cm and 72 cm into identical smaller squares without any waste. The largest possible size of these squares would be the GCF of 28 and 72 (4 cm).
-
Resource Allocation: Imagine dividing a group of 28 students and 72 teachers into smaller groups of equal size. The GCF (4) tells you the largest number of groups that can be formed with an equal number of students and teachers in each group.
Beyond the Basics: Exploring Further Concepts
While we've focused on finding the GCF of 28 and 72, the underlying principles extend to more complex scenarios:
-
Finding the GCF of more than two numbers: The same methods (prime factorization and Euclidean algorithm) can be extended to find the GCF of three or more numbers.
-
Least Common Multiple (LCM): Closely related to the GCF is the LCM, the smallest number that is a multiple of both numbers. The GCF and LCM are related by the formula: GCF(a, b) × LCM(a, b) = a × b.
-
Modular Arithmetic and Cryptography: The GCF plays a vital role in modular arithmetic, which has significant applications in cryptography and secure communication. Concepts like the Euclidean algorithm are fundamental in encryption and decryption algorithms.
Conclusion: The Power of the Greatest Common Factor
Finding the greatest common factor of 28 and 72, as demonstrated through various methods, reveals the fundamental importance of this concept in number theory and its practical applications. From simplifying fractions to solving complex equations and optimizing resource allocation, the GCF provides a powerful tool for understanding and solving problems across multiple disciplines. Understanding the various methods for calculating the GCF equips you with essential mathematical skills applicable in numerous contexts. The Euclidean algorithm, in particular, showcases the elegance and efficiency of mathematical methods for tackling seemingly complex problems. The ability to quickly and efficiently determine the greatest common factor is a skill that transcends simple arithmetic and lays a foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
How Long Should It Take To Read 50 Pages
May 09, 2025
-
Fractions That Are Equivalent To 8 12
May 09, 2025
-
400 Is What Percent Of 500
May 09, 2025
-
How Many Tsp Is 1 Garlic Clove
May 09, 2025
-
How Many Years Ago Was 1700
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 28 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.