What Is The Greatest Common Factor Of 72 And 40
Treneri
May 12, 2025 · 5 min read
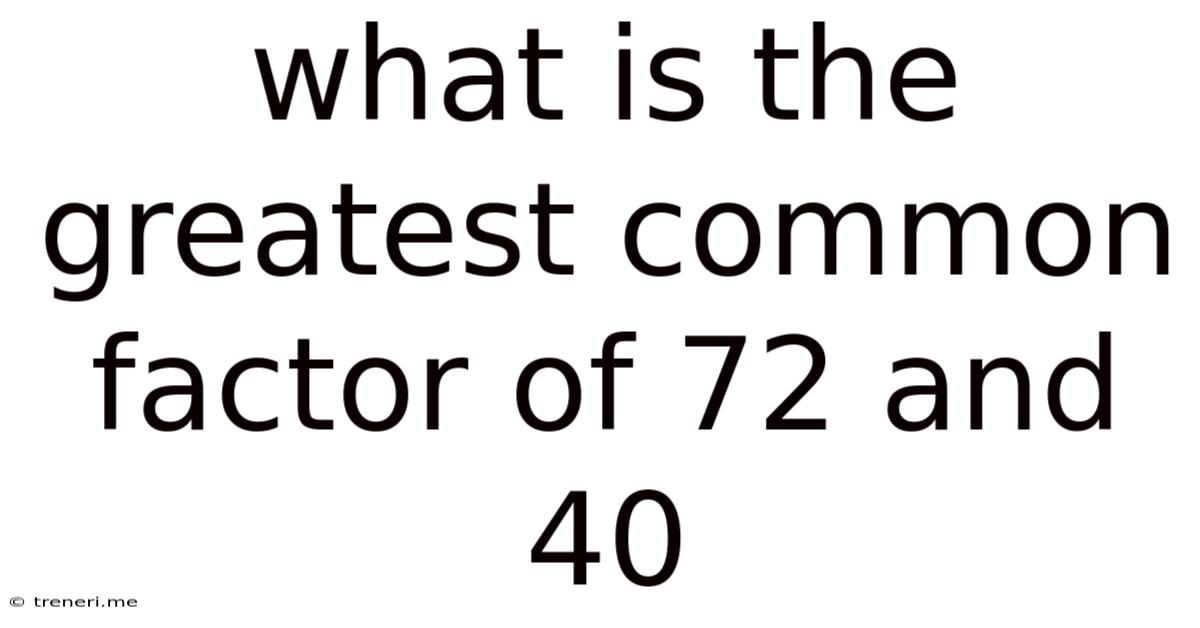
Table of Contents
What is the Greatest Common Factor of 72 and 40? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a concept with far-reaching implications in mathematics and beyond. This article will not only answer the question of what the GCF of 72 and 40 is, but will also explore the various methods for finding it, delve into its practical applications, and connect it to broader mathematical concepts.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and working with various geometric problems.
Methods for Finding the GCF of 72 and 40
Several methods can be used to determine the GCF of 72 and 40. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the lists, we see that the common factors are 1, 2, 4, and 8. The greatest among these is 8. Therefore, the GCF of 72 and 40 is 8.
This method works well for smaller numbers but becomes cumbersome with larger ones.
2. Prime Factorization
This method utilizes the prime factorization of each number. The prime factorization of a number is its expression as a product of prime numbers.
- Prime factorization of 72: 2³ x 3² (2 x 2 x 2 x 3 x 3)
- Prime factorization of 40: 2³ x 5 (2 x 2 x 2 x 5)
To find the GCF, we identify the common prime factors and their lowest powers. Both numbers share three factors of 2 (2³). Therefore, the GCF is 2³ = 8.
Prime factorization is a more efficient method for larger numbers, especially when dealing with numbers having many factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for large numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal.
Let's apply the Euclidean algorithm to 72 and 40:
- 72 = 40 x 1 + 32
- 40 = 32 x 1 + 8
- 32 = 8 x 4 + 0
The last non-zero remainder is the GCF. Therefore, the GCF of 72 and 40 is 8.
The Euclidean algorithm is significantly more efficient than the previous methods for larger numbers because it avoids the need to find all factors. It's an elegant and powerful technique rooted in the principles of number theory.
Applications of GCF
The concept of GCF extends far beyond simple arithmetic exercises. Here are some significant applications:
1. Simplifying Fractions
GCF is fundamental to simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, to simplify the fraction 72/40, we divide both by their GCF (8):
72/40 = (72 ÷ 8) / (40 ÷ 8) = 9/5
2. Solving Word Problems
Many word problems involve finding the GCF. Consider a scenario where you have 72 red marbles and 40 blue marbles, and you want to divide them into identical bags with the same number of red and blue marbles in each bag. The largest number of bags you can make is determined by the GCF of 72 and 40, which is 8.
3. Geometry
GCF plays a role in geometry, especially when dealing with problems involving area and dimensions. For example, if you need to tile a rectangular floor with square tiles, the size of the largest square tile that fits perfectly is determined by the GCF of the floor's dimensions.
4. Algebra
GCF is essential in simplifying algebraic expressions. For instance, consider the expression 72x + 40y. The GCF of 72 and 40 is 8, so the expression can be simplified to 8(9x + 5y).
5. Cryptography
While not directly apparent, GCF plays a crucial role in some aspects of cryptography, particularly in algorithms involving modular arithmetic and prime factorization. Understanding GCF is fundamental to grasping the mathematical underpinnings of these security systems.
6. Music Theory
Interestingly, GCF finds application in music theory, specifically in determining the intervals between notes. The GCF helps simplify musical ratios and identify consonant intervals.
Expanding on Number Theory Concepts Related to GCF
The GCF is deeply connected to other core concepts in number theory:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of both numbers. There's a relationship between GCF and LCM: For any two integers a and b, GCF(a, b) x LCM(a, b) = a x b. This property provides a way to efficiently calculate the LCM once the GCF is known.
-
Prime Numbers: Prime numbers are the building blocks of all integers. The prime factorization method for finding the GCF relies directly on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Modular Arithmetic: Modular arithmetic is a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value, called the modulus. The GCF plays a role in determining the properties of modular arithmetic systems, such as the existence of multiplicative inverses.
-
Diophantine Equations: These are equations where only integer solutions are sought. The GCF often plays a crucial role in determining the solvability and solutions of Diophantine equations.
Conclusion: The Importance of Understanding GCF
This in-depth exploration of the greatest common factor demonstrates its significance beyond simple arithmetic. From simplifying fractions to its role in complex mathematical concepts like cryptography and number theory, the GCF is a fundamental building block of mathematical understanding. Mastering the different methods for finding the GCF—listing factors, prime factorization, and the Euclidean algorithm—equips you with powerful tools for solving a wide variety of mathematical problems, highlighting its crucial place in both elementary and advanced mathematics. The seemingly simple question of finding the GCF of 72 and 40 opens up a fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
Least Common Multiple Of 11 And 10
May 12, 2025
-
10 Out Of 21 As A Percentage
May 12, 2025
-
How Much Omega 3 Per Day For Dogs
May 12, 2025
-
7 Out Of 10 As A Grade
May 12, 2025
-
60 Days From November 12 2024
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 72 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.