What Is The Percentage Of 24 Out Of 40
Treneri
May 13, 2025 · 5 min read
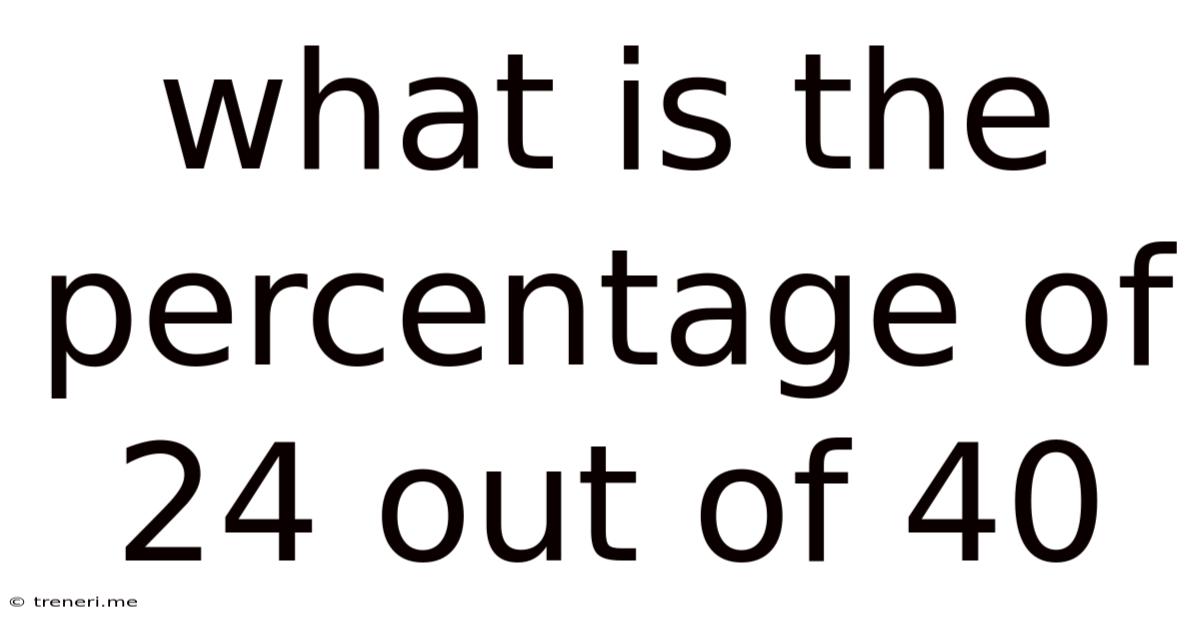
Table of Contents
What is the Percentage of 24 out of 40? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various fields, from finance and statistics to everyday life. Understanding how to determine percentages allows you to interpret data, make informed decisions, and effectively communicate proportions. This article delves into the specifics of calculating the percentage of 24 out of 40, explaining the process step-by-step and expanding on broader percentage concepts. We'll explore different methods, offer practical examples, and provide you with the tools to confidently tackle any percentage calculation.
Understanding Percentages
Before we jump into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Calculating the Percentage of 24 out of 40: The Step-by-Step Method
To find the percentage of 24 out of 40, we follow these straightforward steps:
Step 1: Set up the Fraction
First, we express the given numbers as a fraction. The number we're finding the percentage of (40) goes in the denominator (the bottom part of the fraction), and the number we're interested in (24) goes in the numerator (the top part of the fraction):
24/40
Step 2: Convert the Fraction to a Decimal
Next, we divide the numerator by the denominator:
24 ÷ 40 = 0.6
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, we multiply by 100 and add the "%" symbol:
0.6 x 100 = 60%
Therefore, 24 out of 40 is 60%.
Alternative Methods for Percentage Calculation
While the above method is the most straightforward, there are alternative approaches that can be useful depending on the context and your comfort level with different mathematical operations.
Method 2: Using Proportions
This method leverages the concept of proportional relationships. We can set up a proportion to solve for the unknown percentage (x):
24/40 = x/100
To solve for x, we cross-multiply:
40x = 2400
Then, divide both sides by 40:
x = 2400/40 = 60
Therefore, x = 60%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply enter 24 ÷ 40 and then multiply by 100. The calculator will directly provide the answer as 60%. This method is especially helpful for more complex calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for navigating various real-world scenarios. Here are some examples:
-
Academic Performance: If you scored 24 out of 40 on a test, your score is 60%. This allows you to understand your performance relative to the total possible marks.
-
Sales and Discounts: A store offering a 60% discount on an item means that you will pay 40% of the original price. This type of calculation is essential for budgeting and shopping.
-
Financial Analysis: In finance, percentages are used extensively to track interest rates, investment returns, and profit margins. Understanding percentage change helps in analyzing financial trends.
-
Data Analysis and Statistics: Percentages are fundamental in statistical analysis, enabling us to represent data proportions, calculate probabilities, and interpret survey results.
-
Everyday Life: From calculating tips in restaurants to understanding tax rates, percentages are integral to numerous daily activities.
Beyond the Basics: Understanding Percentage Increase and Decrease
While calculating the percentage of a given value is important, understanding percentage change (increase or decrease) is equally crucial. Let's consider examples related to our original problem:
Percentage Increase: Suppose you initially had 24 items and now have 40. What is the percentage increase?
- Find the difference: 40 - 24 = 16
- Divide the difference by the original value: 16/24 = 0.6667
- Multiply by 100 to get the percentage: 0.6667 x 100 ≈ 66.67%
Therefore, there is approximately a 66.67% increase.
Percentage Decrease: Now, suppose you started with 40 items and now have 24. What is the percentage decrease?
- Find the difference: 40 - 24 = 16
- Divide the difference by the original value: 16/40 = 0.4
- Multiply by 100 to get the percentage: 0.4 x 100 = 40%
Therefore, there is a 40% decrease.
Troubleshooting Common Percentage Calculation Errors
Even with straightforward calculations, errors can occur. Here are some common mistakes to avoid:
-
Incorrect Order of Operations: Always ensure you perform the division before the multiplication when converting a fraction to a percentage.
-
Misinterpretation of the Problem: Carefully read the problem to identify the correct values for the numerator and denominator. The context is critical.
-
Decimal Point Errors: Be meticulous with decimal points during the conversion from decimal to percentage. A misplaced decimal point will drastically alter the result.
-
Rounding Errors: When dealing with decimals, you may need to round to a specific number of decimal places. Be consistent in your rounding method to avoid inaccuracies.
Conclusion: Mastering Percentage Calculations for Success
The ability to calculate percentages is a valuable skill with far-reaching applications. Understanding the methods, recognizing real-world contexts, and avoiding common errors will empower you to confidently handle percentage calculations in various situations – from academic assignments and financial planning to daily decision-making. By mastering this fundamental mathematical skill, you’ll gain a significant advantage in navigating the quantitative aspects of life. Remember that practice is key. The more you work with percentage calculations, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
How Many Pounds Is 15 Grams
May 13, 2025
-
How To Calculate Average Fixed Manufacturing Cost Per Unit
May 13, 2025
-
What Is 0 7 To The Power Of 2
May 13, 2025
-
Greatest Common Factor Of 45 And 120
May 13, 2025
-
How Many More Hours Till 6 00
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 24 Out Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.