What Is The Square Root Of 31
Treneri
Apr 05, 2025 · 4 min read
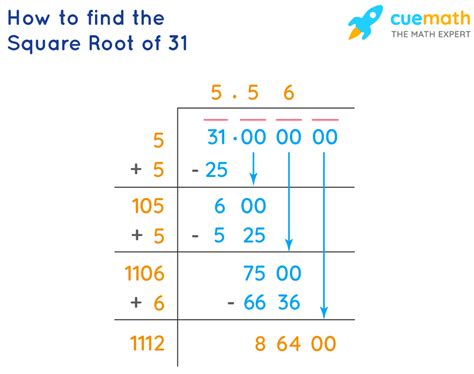
Table of Contents
What is the Square Root of 31? A Deep Dive into Irrational Numbers and Approximation Techniques
The question, "What is the square root of 31?" seems simple enough. However, delving into its answer opens a fascinating window into the world of mathematics, specifically irrational numbers and the various methods used to approximate their values. This comprehensive guide will not only provide you with the answer but also explore the underlying concepts and practical applications.
Understanding Square Roots
Before we tackle the square root of 31, let's solidify our understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This is also written as 3².
The Square Root of 31: An Irrational Number
Unlike the square root of 9, the square root of 31 (√31) is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating. This is a fundamental characteristic of many numbers in mathematics and is crucial to understanding its value.
Key Characteristics of Irrational Numbers:
- Non-terminating and Non-repeating Decimals: The decimal representation continues infinitely without any discernible pattern.
- Cannot be expressed as a fraction: They cannot be written as the ratio of two whole numbers.
- Ubiquitous in Mathematics: They appear frequently in geometry, trigonometry, and calculus.
Approximating √31: Methods and Techniques
Since we cannot express √31 exactly, we must resort to approximation methods. Several techniques exist, each with varying levels of accuracy and complexity.
1. Using a Calculator
The simplest way to find an approximation is by using a calculator. Most calculators have a square root function (√). Inputting √31 will give you a decimal approximation, typically accurate to several decimal places. For example, a calculator might display:
√31 ≈ 5.56776436283
While convenient, a calculator doesn't illuminate the underlying mathematical principles.
2. The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation of the square root. It involves repeatedly refining an initial guess using the formula:
x_(n+1) = (x_n + S/x_n) / 2
Where:
- x_n is the current approximation.
- x_(n+1) is the next, improved approximation.
- S is the number whose square root is being sought (in this case, 31).
Steps:
- Make an initial guess: Let's start with x_0 = 6 (since 6² = 36, which is close to 31).
- Apply the formula:
- x_1 = (6 + 31/6) / 2 ≈ 5.5833
- x_2 = (5.5833 + 31/5.5833) / 2 ≈ 5.5678
- x_3 = (5.5678 + 31/5.5678) / 2 ≈ 5.56776
As you can see, the approximation converges quickly towards the actual value. The more iterations you perform, the greater the accuracy.
3. Using Linear Approximation
This method leverages the tangent line of a function to estimate the value. Consider the function f(x) = x². The square root of 31 is the x-value where f(x) = 31. We can use a known point close to √31, such as x = 6 (f(6) = 36). The tangent line at x = 6 can provide a reasonable approximation.
The equation of the tangent line at x = 6 is:
y - 36 = 12(x - 6)
Setting y = 31, we can solve for x:
31 - 36 = 12(x - 6)
x ≈ 5.4167
This method, while simpler than the Babylonian method, yields a less accurate approximation.
4. Numerical Methods (Newton-Raphson Method)
For higher accuracy and more complex scenarios, numerical methods like the Newton-Raphson method are employed. These methods use iterative calculations to refine an initial guess, converging to a solution within a desired tolerance. While more sophisticated, their implementation often requires programming or specialized software.
Applications of √31
While √31 might not seem immediately practical, irrational numbers like it frequently appear in various applications:
- Geometry: Calculating the diagonal of a rectangle or the hypotenuse of a right-angled triangle often involves irrational numbers. If a rectangle has sides of length 5 and 2, the diagonal would involve √31.
- Physics: Many physical phenomena are described by equations involving square roots. For example, calculations relating to velocity, acceleration, and energy often involve irrational numbers.
- Engineering: In structural engineering and design, calculations for stability, stress, and strain might involve irrational numbers.
- Computer Graphics: Generating realistic images and animations often requires extensive mathematical calculations, including square roots.
- Financial Modeling: Calculating compound interest or determining investment returns might involve the use of irrational numbers in more complex scenarios.
Conclusion: Embracing the Irrational
The square root of 31, while an irrational number and therefore impossible to express precisely as a decimal, is a perfectly valid and useful mathematical entity. Understanding its irrationality, alongside the various methods for approximation, provides a deeper understanding of the complexities and beauty inherent within mathematics. From the simple calculator approximation to the iterative precision of the Babylonian method, several techniques allow us to work effectively with irrational numbers in a wide range of applications. The inability to express it perfectly as a decimal does not diminish its significance or utility within the mathematical world and beyond. It serves as a reminder that many fundamental constants and relationships in our world are beautifully and inherently irrational.
Latest Posts
Latest Posts
-
How To Calculate Urine Protein Creatinine Ratio
Apr 05, 2025
-
How Many Milliseconds Are In 1 Second
Apr 05, 2025
-
1 2 Cup Cooked Rice Is How Much Dry
Apr 05, 2025
-
50000 Pennies Equals How Many Dollars
Apr 05, 2025
-
How Many Hours Is 20000 Minutes
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
