What Is To The -1/2 Power
Treneri
Apr 07, 2025 · 5 min read
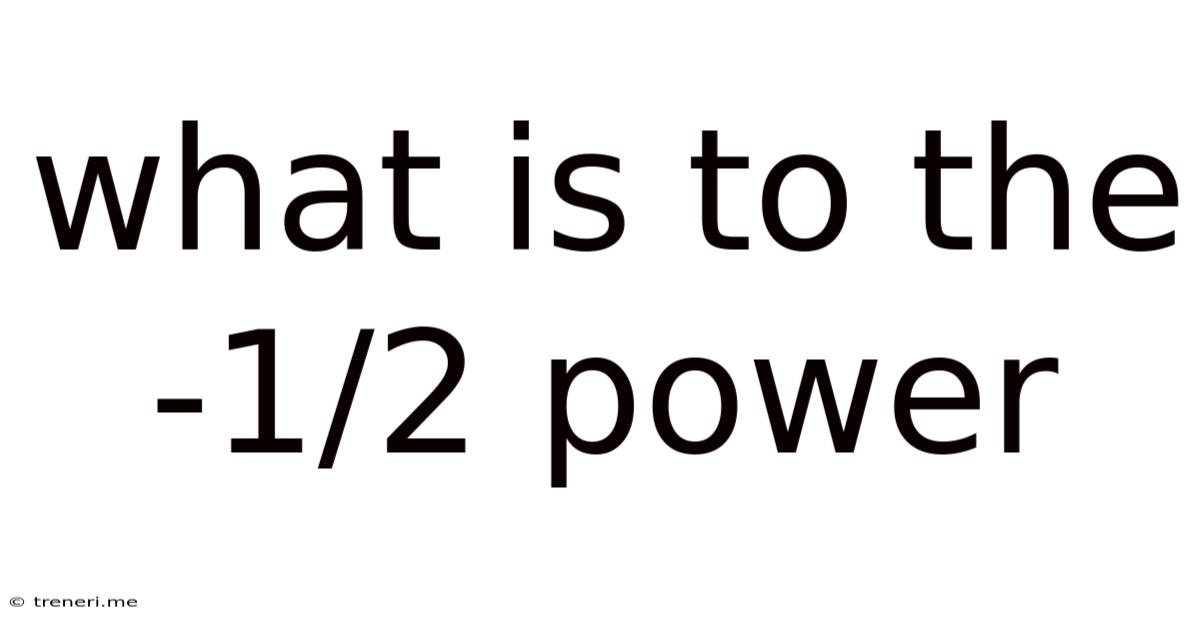
Table of Contents
What is to the -1/2 Power? A Comprehensive Guide
Understanding exponents, especially fractional and negative ones, can feel daunting. But fear not! This comprehensive guide will demystify the meaning and application of raising a number to the -1/2 power. We'll break down the concept step-by-step, exploring its mathematical basis and practical applications. By the end, you'll be confident in tackling this seemingly complex mathematical operation.
Understanding Exponents: A Quick Refresher
Before diving into the specifics of the -1/2 power, let's refresh our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- x² means x * x (x multiplied by itself twice)
- x³ means x * x * x (x multiplied by itself three times)
- x⁴ means x * x * x * x (and so on)
Deconstructing the -1/2 Power
The expression "to the -1/2 power" combines two key concepts: negative exponents and fractional exponents. Let's tackle each separately.
Negative Exponents
A negative exponent signifies the reciprocal of the base raised to the positive exponent. In simpler terms, it means "flip the fraction" and change the sign of the exponent. For example:
- x⁻¹ = 1/x (The reciprocal of x)
- x⁻² = 1/x² (The reciprocal of x²)
- x⁻³ = 1/x³ (And so on)
This rule applies to any base, whether it's a number, a variable, or a more complex expression.
Fractional Exponents
A fractional exponent represents a combination of two operations: exponentiation and root extraction. The numerator of the fraction indicates the power to which the base is raised, while the denominator indicates the root to be taken. For example:
- x^(1/2) = √x (The square root of x)
- x^(1/3) = ³√x (The cube root of x)
- x^(1/n) = n√x (The nth root of x)
So, x raised to the power of 1/n is the same as taking the nth root of x.
Putting it Together: The -1/2 Power
Now, let's combine these concepts to understand the -1/2 power. The expression x⁻¹/² can be broken down as follows:
-
The negative exponent: This tells us to take the reciprocal of the base raised to the positive exponent (1/2).
-
The fractional exponent (1/2): This indicates that we need to take the square root of the base.
Therefore, x⁻¹/² = 1/√x or 1/x¹/². This means we take the square root of x and then find the reciprocal of the result.
Examples: Bringing it to Life
Let's illustrate this with some numerical examples:
Example 1: Calculate 9⁻¹/².
- Fractional exponent: We first calculate the square root of 9, which is 3 (√9 = 3).
- Negative exponent: Then, we take the reciprocal of 3, which is 1/3.
Therefore, 9⁻¹/² = 1/3.
Example 2: Calculate 16⁻¹/².
- Fractional exponent: The square root of 16 is 4 (√16 = 4).
- Negative exponent: The reciprocal of 4 is 1/4.
Therefore, 16⁻¹/² = 1/4.
Example 3: Calculate (1/25)⁻¹/²
- Negative exponent: First we address the negative exponent by taking the reciprocal: This gives us 25¹/².
- Fractional exponent: Then we calculate the square root of 25: √25 = 5.
Therefore, (1/25)⁻¹/² = 5.
Example 4: Calculating with Variables: Simplify (4x²)⁻¹/²
- Negative Exponent: First take the reciprocal: 1/(4x²)¹/²
- Fractional Exponent (Square Root): Next, we apply the square root to both the numerator and denominator: 1/(√4 * √x²) which simplifies to 1/(2x)
Therefore, (4x²)⁻¹/² = 1/(2x)
Practical Applications
While the -1/2 power might seem abstract, it has practical applications in various fields:
-
Physics: It often appears in formulas related to inverse square laws, such as the intensity of light or gravitational force. The inverse square relationship often involves a term raised to the power of -2, but the -1/2 power can arise when manipulating these equations.
-
Statistics: The -1/2 power might be encountered in statistical calculations involving standard deviations and probability distributions.
-
Finance: Financial models, especially those dealing with discounting or present value calculations, can utilize fractional exponents to model the time value of money.
-
Engineering: This exponent can arise in various engineering calculations when dealing with inverse relationships or scaling problems.
-
Computer Science: In algorithms and data structures that deal with scaling or inverse relationships, the -1/2 power might appear in the complexity analysis.
Working with More Complex Expressions
The principles discussed above can be extended to more complex expressions. Remember the order of operations (PEMDAS/BODMAS) when dealing with multiple operations. Always address the exponent before performing any other arithmetic operation.
Avoiding Common Mistakes
-
Order of operations: Remember to follow the correct order of operations when evaluating expressions. Deal with exponents before multiplication, division, addition, or subtraction.
-
Signs: Pay close attention to the signs of the exponents and the base. A negative exponent means reciprocal, not a negative number.
-
Fractional Exponents: Remember the numerator represents the power and the denominator represents the root.
Conclusion
The -1/2 power, while initially seeming complex, is simply a combination of taking the reciprocal and the square root. By understanding the concepts of negative and fractional exponents, you can confidently tackle this operation and apply it in various mathematical and scientific contexts. With practice and a clear understanding of the underlying principles, you'll master this crucial aspect of algebra and unlock a deeper understanding of mathematics. Remember to break down complex problems into smaller, manageable steps, always applying the correct order of operations. This systematic approach will empower you to solve more complex mathematical problems and advance your skills.
Latest Posts
Latest Posts
-
1500 Ml Is How Many Cups
May 09, 2025
-
How Big Is My Trash Can
May 09, 2025
-
Circumference Of A 10 Foot Circle
May 09, 2025
-
X 2 3 In Radical Form
May 09, 2025
-
550 Km Is How Many Miles
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is To The -1/2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.