What Percent Of 10 Is 2
Treneri
May 14, 2025 · 5 min read
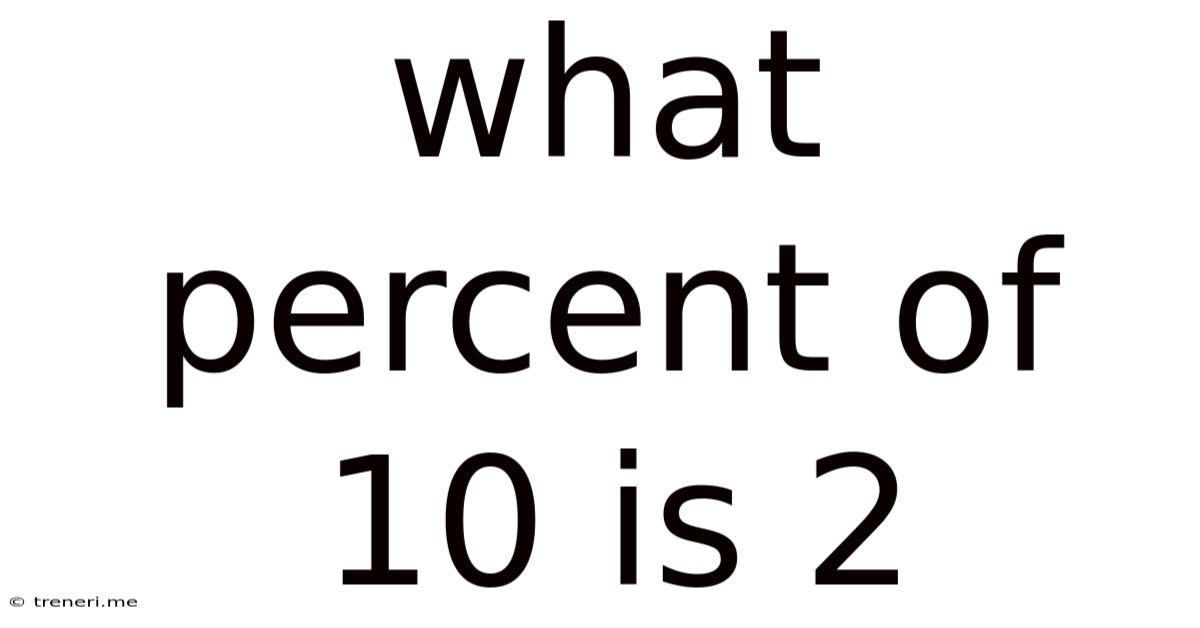
Table of Contents
What Percent of 10 is 2? A Deep Dive into Percentages
Finding the percentage one number represents of another is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial reports. This article will thoroughly explore the question, "What percent of 10 is 2?" We'll not only solve this specific problem but also delve into the underlying concepts and methods, providing you with a comprehensive understanding of percentages and equipping you with the tools to tackle similar problems with confidence.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 25% means 25 out of 100, which can also be expressed as the fraction 25/100 or the decimal 0.25. Percentages are a convenient way to represent proportions and comparisons.
Key Concepts:
- Part: This is the number we're interested in finding the percentage of. In our example, "2" is the part.
- Whole: This is the total amount or the base number to which the part is compared. Here, "10" is the whole.
- Percentage: This is the value we're trying to find, expressed as a number out of 100.
Calculating the Percentage: What Percent of 10 is 2?
There are several ways to solve this problem. Let's explore the most common methods:
Method 1: Using a Proportion
This method uses the concept of equivalent ratios. We set up a proportion:
Part / Whole = Percentage / 100
Substituting our values:
2 / 10 = x / 100
To solve for 'x' (the percentage), we cross-multiply:
2 * 100 = 10 * x
200 = 10x
Divide both sides by 10:
x = 20
Therefore, 2 is 20% of 10.
Method 2: Using Decimal Conversion
This method involves converting the fraction representing the part and the whole into a decimal and then multiplying by 100.
First, express the part as a fraction of the whole:
2 / 10
Simplify the fraction:
1 / 5
Now, convert the fraction to a decimal by dividing the numerator by the denominator:
1 ÷ 5 = 0.2
Finally, multiply the decimal by 100 to express it as a percentage:
0.2 * 100 = 20
Again, we find that 2 is 20% of 10.
Method 3: Using a Formula
We can also use a direct formula:
Percentage = (Part / Whole) * 100
Plugging in our values:
Percentage = (2 / 10) * 100
Percentage = 0.2 * 100
Percentage = 20
This confirms that 2 is 20% of 10.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in many real-world situations. Here are a few examples:
1. Discounts and Sales Tax:
Imagine a shirt costs $10, and it's on sale with a 20% discount. To find the discount amount, you'd calculate 20% of $10, which we've already established is $2. Similarly, calculating sales tax involves finding a percentage of the total cost.
2. Grade Calculations:
Suppose you scored 2 points out of 10 on a quiz. This would be a 20% score. This method is used to calculate grades across various assessments.
3. Financial Analysis:
In finance, percentage calculations are essential. For example, calculating interest rates, profit margins, or return on investment all rely on understanding percentages.
4. Statistics and Data Analysis:
Percentages are frequently used to represent data and trends. For example, survey results often present data as percentages to show proportions of responses. Understanding percentages helps in interpreting and analyzing this type of data effectively.
5. Everyday Comparisons:
We compare things using percentages constantly. For example, "This product is 50% larger than that one." Knowing how to calculate percentages enables accurate comparison and decision-making.
Beyond the Basics: More Complex Percentage Problems
While the example "What percent of 10 is 2?" is straightforward, percentage problems can become more complex. Here are a few examples and how to approach them:
1. Finding the Whole:
If 20% of a number is 2, what is the number?
To solve this, set up the equation:
0.20 * x = 2
Divide both sides by 0.20:
x = 2 / 0.20 = 10
2. Finding the Part:
What is 25% of 20?
Here, we simply multiply the percentage (as a decimal) by the whole:
0.25 * 20 = 5
3. Percentage Increase/Decrease:
If a price increases from $10 to $12, what is the percentage increase?
First, find the difference: $12 - $10 = $2
Then, divide the difference by the original amount and multiply by 100:
($2 / $10) * 100 = 20%
Therefore, there is a 20% increase.
Mastering Percentages: Tips and Practice
Mastering percentage calculations requires practice. Here are some tips to help you:
- Understand the fundamentals: Ensure you grasp the concepts of part, whole, and percentage.
- Use different methods: Experiment with the proportion method, decimal conversion, and the formula to find the method that suits you best.
- Practice regularly: Solve various percentage problems to build your skills and confidence.
- Check your work: Always verify your answers to ensure accuracy.
- Utilize online resources: Numerous websites and apps offer practice problems and tutorials on percentages.
By understanding the concepts and practicing regularly, you'll develop a strong grasp of percentage calculations and confidently apply this essential skill in various aspects of your life. Remember, the key is to break down the problem into smaller, manageable steps, and choosing the method most comfortable for you. The ability to understand and calculate percentages opens doors to understanding a vast array of numerical information and making informed decisions based on data. So, keep practicing, and you'll soon be a percentage pro!
Latest Posts
Latest Posts
-
44 Rounded To The Nearest Ten
May 14, 2025
-
2 Out Of 36 As A Percentage
May 14, 2025
-
58 Rounded To The Nearest Ten
May 14, 2025
-
What Is 50 Basis Points In Mortgage
May 14, 2025
-
45 Days After July 29 2024
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.