What Percent Of 32 Is 12
Treneri
May 10, 2025 · 4 min read
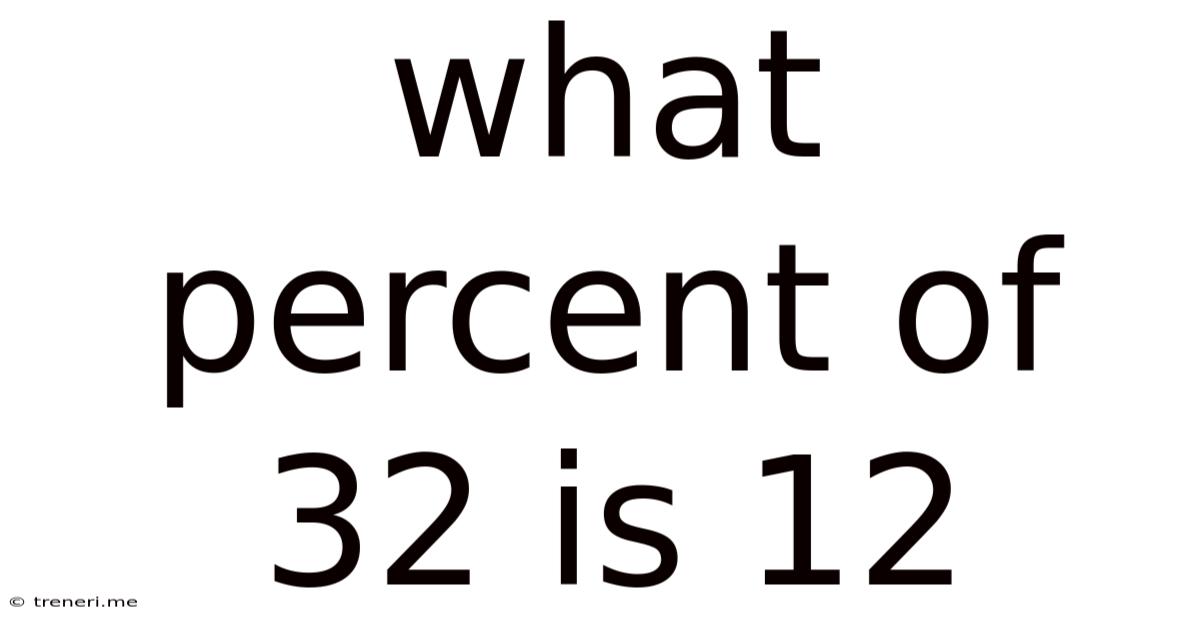
Table of Contents
What Percent of 32 is 12? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific calculations. This article delves into the question, "What percent of 32 is 12?", providing a detailed explanation of the solution, exploring different approaches, and expanding on the broader concept of percentage calculations. We’ll cover various methods, including the formulaic approach, using proportions, and even exploring a practical real-world application. By the end, you'll not only know the answer but also possess a comprehensive understanding of how to tackle similar percentage problems.
Understanding the Problem: What Percent of 32 is 12?
The core of the problem lies in determining the percentage that represents the ratio of 12 to 32. In simpler terms, we need to find what fraction of 32 is equivalent to 12, and then express that fraction as a percentage. This seemingly simple question forms the basis for numerous applications, from calculating discounts and taxes to determining statistical probabilities and analyzing financial data.
Method 1: The Formulaic Approach
The most direct method involves using the fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 12 (the value we're interested in)
- Whole: 32 (the total value)
Substituting these values into the formula:
(12 / 32) * 100% = Percentage
Performing the calculation:
0.375 * 100% = 37.5%
Therefore, 12 is 37.5% of 32.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion where one ratio represents the known values (12 out of 32) and the other ratio represents the unknown percentage (x out of 100):
12/32 = x/100
To solve for x (the percentage), we cross-multiply:
12 * 100 = 32 * x
1200 = 32x
Now, divide both sides by 32:
x = 1200 / 32
x = 37.5
Therefore, x = 37.5%, confirming our previous result.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to obtain the percentage.
- Convert the fraction to a decimal: 12/32 = 0.375
- Multiply by 100%: 0.375 * 100% = 37.5%
This method is straightforward and efficient, particularly when dealing with simpler fractions.
Real-World Application: Understanding Sales Discounts
Imagine a store offering a discount on an item originally priced at $32. The discounted price is $12. To determine the percentage discount, we can use the methods described above.
Following the formula: (Discount/Original Price) * 100% = Percentage Discount
($12/$32) * 100% = 37.5%
The store is offering a 37.5% discount on the item. This understanding of percentage calculations is crucial for consumers to make informed purchasing decisions.
Expanding on Percentage Calculations: Further Concepts
While we've addressed the specific question, let's explore related percentage concepts to strengthen your understanding:
Calculating the Whole from a Percentage and Part
Suppose you know that 37.5% of a certain number is 12. How do you find the original number? We can reverse-engineer the formula:
Percentage = (Part / Whole) * 100%
Rearranging the formula to solve for the Whole:
Whole = (Part / Percentage) * 100
Substituting the known values:
Whole = (12 / 37.5) * 100
Whole = 32
This confirms that the original number was indeed 32. This skill is useful in scenarios where you have a percentage and a part and need to determine the original whole value.
Calculating the Part from a Percentage and Whole
Conversely, if you know the whole (32) and the percentage (37.5%), you can calculate the part (12) using the following formula:
Part = (Percentage/100) * Whole
Part = (37.5/100) * 32
Part = 12
This helps determine the value of a portion when you know the total and the percentage representation of that portion.
Percentage Increase and Decrease
Percentage calculations extend to understanding increases and decreases. For instance, if a value increases from 20 to 25, the percentage increase is calculated as:
((New Value - Original Value) / Original Value) * 100% = Percentage Increase
((25 - 20) / 20) * 100% = 25%
Similarly, for percentage decreases:
((Original Value - New Value) / Original Value) * 100% = Percentage Decrease
These calculations are vital in various applications, such as analyzing financial growth or decline, population changes, or comparing data sets.
Troubleshooting Common Percentage Errors
Common mistakes in percentage calculations include:
- Incorrect order of operations: Always remember the order of operations (PEMDAS/BODMAS).
- Confusing percentage and decimal: Ensure you convert decimals to percentages and vice-versa correctly.
- Misinterpreting the problem: Clearly define the 'part' and 'whole' before applying the formula.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with widespread applications. Through various methods, from the formulaic approach to utilizing proportions and decimal conversions, we've explored how to determine "What percent of 32 is 12?" This detailed explanation, coupled with real-world examples and explanations of related concepts, equips you to confidently tackle any percentage problem. Understanding percentage calculations allows you to navigate financial matters, analyze data effectively, and solve various problems across different domains with greater accuracy and efficiency. Remember to practice regularly and apply these techniques in diverse scenarios to build a strong foundational understanding. By consistently practicing these methods, you'll develop a keen intuition for percentages and their role in interpreting data and solving practical problems.
Latest Posts
Latest Posts
-
What Is A 27 Out Of 31
May 10, 2025
-
How Is True Shooting Percentage Calculated
May 10, 2025
-
Can You Tan With A Uv Of 3
May 10, 2025
-
What Is The Gcf Of 3 And 18
May 10, 2025
-
How Much Is 330ml In Cups
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 32 Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.