What Percent Of 500 Is 200
Treneri
Apr 13, 2025 · 5 min read
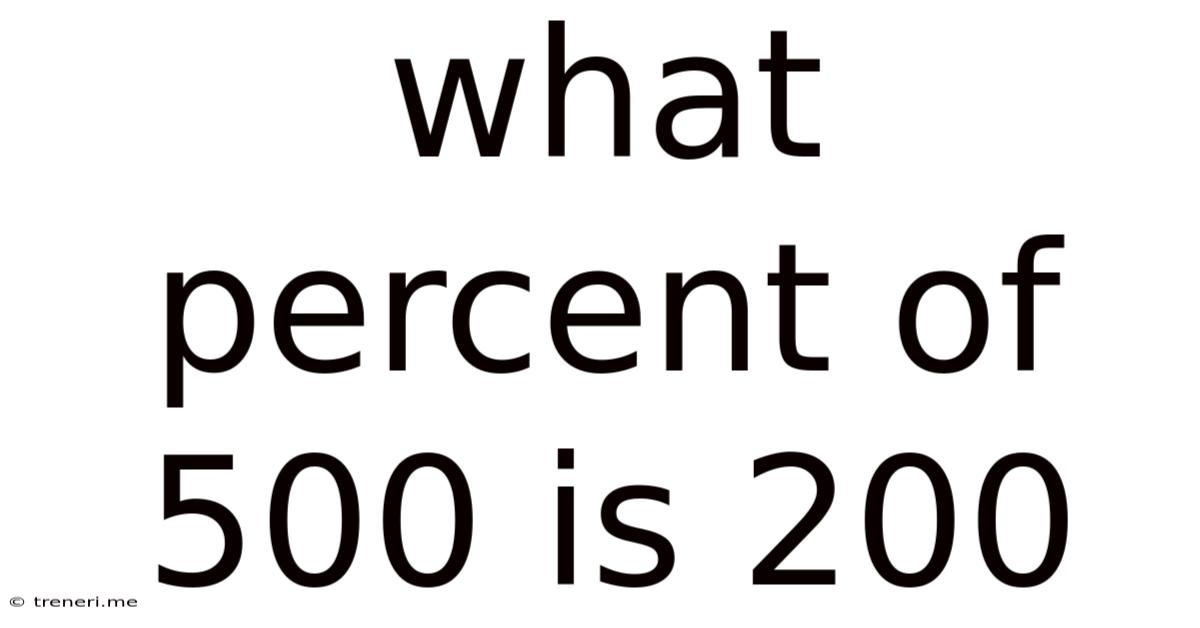
Table of Contents
What Percent of 500 is 200? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 500 is 200?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for anyone looking to master this fundamental concept. This article will not only answer the question directly but also delve into the various methods for solving percentage problems, practical applications, and even touch upon the historical context of percentages.
Understanding Percentages: A Foundation
Before we tackle the core question, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." So, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. This seemingly basic concept forms the bedrock of countless applications in finance, statistics, science, and everyday life.
Method 1: Using the Percentage Formula
The most direct method to answer "What percent of 500 is 200?" involves using the fundamental percentage formula:
(Part / Whole) x 100 = Percentage
In our case:
- Part: 200 (the number we're considering as a percentage of 500)
- Whole: 500 (the total amount)
Plugging these values into the formula:
(200 / 500) x 100 = 40%
Therefore, 200 is 40% of 500.
Method 2: Setting up a Proportion
Another effective approach is setting up a proportion. A proportion is an equation that states that two ratios are equal. We can represent the problem as:
200/500 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
200 * 100 = 500 * x
20000 = 500x
x = 20000 / 500
x = 40
Again, this confirms that 200 is 40% of 500.
Method 3: Using Decimal Equivalents
We can also approach this using decimal equivalents. First, express the fraction 200/500 as a decimal by performing the division:
200 / 500 = 0.4
Then, to convert this decimal to a percentage, multiply by 100:
0.4 x 100 = 40%
This method reinforces the connection between decimals, fractions, and percentages.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just an academic exercise; it's a critical life skill. Consider these examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentages. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase is essential for informed financial decisions.
-
Statistics: Percentages are ubiquitous in data analysis and statistical reporting. Representing survey results, population demographics, and experimental outcomes often uses percentages to provide a clear and concise summary of the data. Understanding these percentages is key to interpreting the information accurately.
-
Science: Many scientific measurements and calculations involve percentages. For example, expressing the concentration of a solution, the efficiency of a process, or the error in a measurement often requires percentage calculations.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, determining the nutritional value of food, and interpreting sports statistics all involve percentages. Being comfortable with percentage calculations simplifies everyday decision-making.
Beyond the Basics: More Complex Percentage Problems
While "What percent of 500 is 200?" is a straightforward problem, percentage calculations can become more intricate. Here are a few examples of more complex scenarios:
-
Finding the Whole: "40% of what number is 200?" This requires rearranging the percentage formula to solve for the "whole."
-
Finding the Part: "What is 60% of 800?" This involves directly applying the percentage formula to find the "part."
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers, such as the percentage increase in sales or the percentage decrease in price. These often require an understanding of absolute change and relative change.
-
Compound Percentages: These involve applying percentages repeatedly, as seen in compound interest calculations. Understanding the effect of compounding over time is crucial in various financial contexts.
Historical Context: The Evolution of Percentages
The concept of percentages has ancient roots. While the specific symbol "%" emerged relatively recently, the underlying idea of expressing fractions as parts of a hundred was used by Roman tax collectors centuries ago. The modern notation, however, solidified during the 17th century. Its widespread adoption was largely driven by the growing need for efficient financial calculations and data representation. The simplicity and universality of percentages made them a preferred tool for expressing proportions and facilitating comparisons.
Mastering Percentages: Tips and Resources
Mastering percentages requires practice. Here are some tips to improve your skills:
- Practice regularly: Solve various percentage problems to build confidence and familiarity with the different methods.
- Visual aids: Use diagrams, charts, or other visual tools to represent percentage relationships. This can make understanding complex problems easier.
- Online resources: Utilize online calculators, tutorials, and practice exercises to reinforce your learning.
- Real-world applications: Apply your knowledge to real-world scenarios to solidify your understanding and improve your problem-solving abilities.
In conclusion, the answer to "What percent of 500 is 200?" is unequivocally 40%. However, this seemingly simple question opens doors to a vast landscape of mathematical concepts and their profound impact on various aspects of our lives. By understanding the fundamental principles of percentages and exploring the different methods of calculation, we equip ourselves with a powerful tool for navigating the complexities of finance, statistics, science, and everyday decision-making. So, go forth and confidently tackle those percentage problems!
Latest Posts
Latest Posts
-
1 2 6 As A Fraction
May 10, 2025
-
128 Rounded To The Nearest Hundred
May 10, 2025
-
Thwyl Alwzn Mn Kylw Ala Bawnd
May 10, 2025
-
90k A Year Is How Much An Hour
May 10, 2025
-
What Percentage Is 10 Out Of 18
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 500 Is 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.