What Percentage Is 10 Out Of 18
Treneri
May 10, 2025 · 4 min read
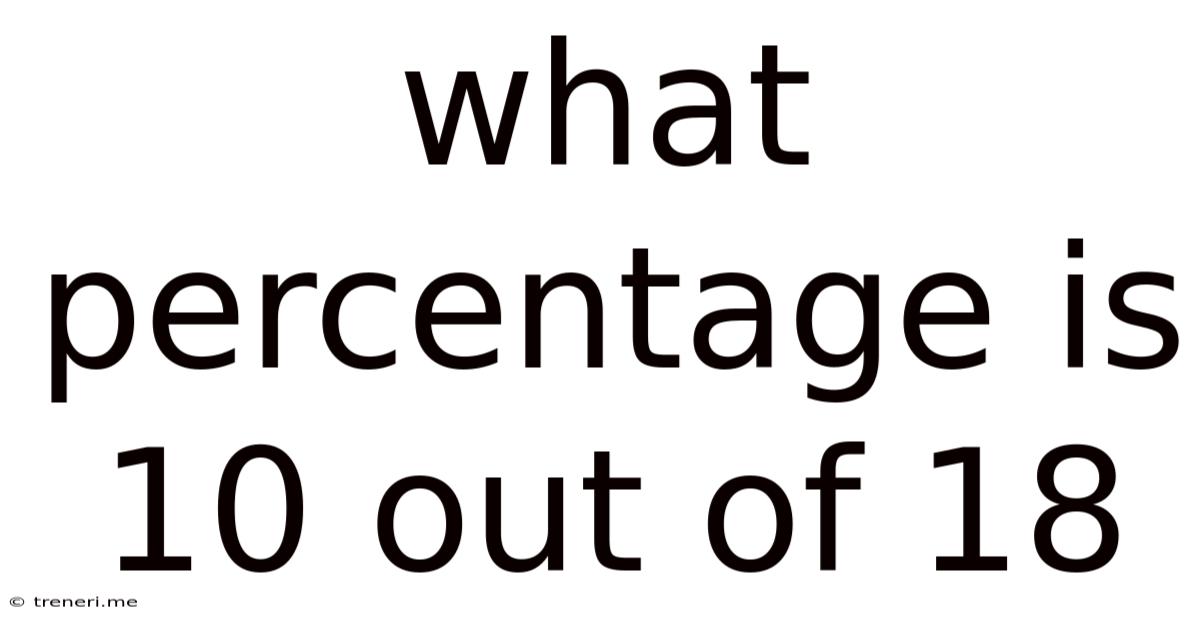
Table of Contents
What Percentage is 10 out of 18? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and tips to analyzing data and understanding financial reports. This comprehensive guide will not only answer the question, "What percentage is 10 out of 18?" but also equip you with the knowledge and tools to calculate percentages confidently and efficiently in any scenario.
Calculating the Percentage: 10 out of 18
The core of percentage calculation lies in understanding the relationship between a part and a whole. In our case, 10 is the part, and 18 is the whole. To find the percentage, we follow these steps:
1. Divide the Part by the Whole:
This step establishes the ratio of the part to the whole. In this instance:
10 ÷ 18 = 0.5556 (approximately)
2. Multiply the Result by 100:
Multiplying the decimal result by 100 converts the ratio into a percentage.
0.5556 x 100 = 55.56%
Therefore, 10 out of 18 is approximately 55.56%.
Understanding the Concept of Percentages
A percentage represents a fraction of 100. It's a way of expressing a proportion or ratio as a fraction of 100. The symbol "%" denotes a percentage. For example:
- 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
- 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
- 100% represents the whole or entirety.
Different Methods for Calculating Percentages
While the method described above is the most straightforward, several other methods can be used depending on the context and your preference.
Method 2: Using Proportions
Percentages can also be calculated using proportions. We set up a proportion where x represents the unknown percentage:
x/100 = 10/18
To solve for x, we cross-multiply:
18x = 1000
x = 1000/18
x ≈ 55.56%
This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using a Calculator
Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 10 ÷ 18 x 100 and press the % button. The calculator will automatically display the result as 55.56%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world situations. Here are a few examples:
1. Sales and Discounts:
Retail stores frequently offer discounts expressed as percentages. For instance, a 20% discount on a $100 item means you'll pay $80 (100 - 20% of 100).
2. Taxes and Interest:
Calculating sales tax, income tax, or interest on loans involves percentage calculations. For example, a 6% sales tax on a $50 purchase would be $3.
3. Grades and Scores:
Percentage calculations are essential in determining grades in educational settings. A score of 15 out of 20 translates to 75%.
4. Financial Analysis:
Investors and financial analysts use percentages to analyze financial statements, growth rates, and investment returns.
5. Data Analysis and Statistics:
Percentages are frequently used in data analysis to represent proportions, trends, and changes within datasets. For example, understanding market share often involves percentage calculations.
Beyond the Basics: Advanced Percentage Problems
While calculating "What percentage is 10 out of 18?" is a fundamental problem, let's explore some more advanced scenarios:
1. Percentage Increase and Decrease:
These calculations determine the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100
For example, if a product's price increased from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100 = 20%
2. Finding the Original Value:
Suppose you know the final value after a percentage increase or decrease, and you want to find the original value. You'll need to work backward using the percentage change.
3. Percentage Points vs. Percentages:
It's crucial to differentiate between percentage points and percentages. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Tips and Tricks for Accurate Percentage Calculations
- Double-check your calculations: It's easy to make mistakes, especially with decimals. Always double-check your work.
- Use a calculator: Calculators are incredibly helpful for quick and accurate calculations.
- Break down complex problems: If a problem seems overwhelming, break it down into smaller, more manageable steps.
- Practice regularly: The more you practice, the more comfortable and confident you'll become with percentage calculations.
Conclusion: Mastering Percentages for Success
Understanding percentages is a vital life skill with applications across numerous fields. This guide provided a comprehensive explanation of how to calculate percentages, including different methods and practical examples. By mastering these techniques, you'll be well-equipped to tackle various percentage-related problems with confidence and precision, whether it's calculating discounts, analyzing data, or making informed financial decisions. Remember to practice regularly, and soon, you'll be a percentage calculation pro!
Latest Posts
Latest Posts
-
1100 Watt To 700 Watt Microwave Conversion
May 11, 2025
-
2500 Pies Cuadrados A Metros Cuadrados
May 11, 2025
-
10 Trillion Divided By 500 Billion
May 11, 2025
-
How To Work Out Tensile Stress
May 11, 2025
-
Common Denominator Of 3 And 6
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 10 Out Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.