What Percent Of 7 Is 3
Treneri
May 12, 2025 · 5 min read
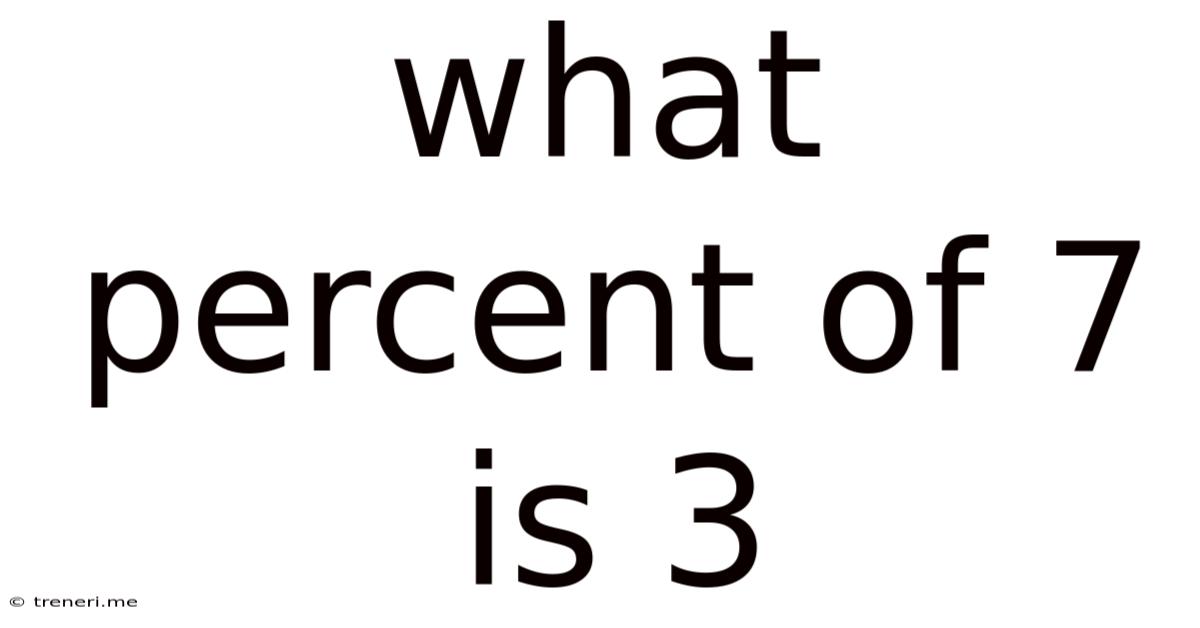
Table of Contents
What Percent of 7 is 3? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in daily life, from calculating discounts and taxes to comprehending statistics and financial reports. This article will thoroughly explore the question, "What percent of 7 is 3?", not just providing the answer but delving into the underlying concepts, different methods for solving similar problems, and exploring real-world applications.
Understanding Percentages: The Basics
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, which can also be represented as the fraction 50/100 or the decimal 0.5.
Percentages are used to express proportions or parts of a whole. They provide a standardized way to compare different quantities or fractions, regardless of their original denominators. This makes percentages particularly useful for making comparisons and drawing conclusions from data.
Method 1: Using Proportions to Solve "What percent of 7 is 3?"
This method utilizes the concept of proportions, which states that two ratios are equal. We can set up a proportion to solve our problem:
x/100 = 3/7
Where 'x' represents the percentage we are trying to find.
To solve for x, we cross-multiply:
7x = 300
Now, divide both sides by 7:
x = 300/7
x ≈ 42.86
Therefore, 3 is approximately 42.86% of 7.
Method 2: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our case:
- Part = 3
- Whole = 7
Substituting these values into the formula:
(3/7) * 100 ≈ 42.86%
This confirms our previous result. This method is straightforward and easy to remember, making it a preferred approach for many percentage calculations.
Method 3: Converting to Decimal and then to Percentage
This method involves first expressing the fraction as a decimal and then converting the decimal to a percentage.
-
Express as a Fraction: The fraction representing "3 out of 7" is 3/7.
-
Convert to Decimal: Divide 3 by 7: 3 ÷ 7 ≈ 0.4286
-
Convert to Percentage: Multiply the decimal by 100: 0.4286 * 100 ≈ 42.86%
This method highlights the relationship between fractions, decimals, and percentages, reinforcing the interconnectedness of these mathematical concepts.
Rounding and Precision
In the above calculations, we rounded the answer to two decimal places (42.86%). The level of precision required depends on the context. In some cases, a whole number percentage might suffice; in others, greater accuracy is necessary. For example, in financial calculations, precision is often critical, whereas in everyday estimations, rounding might be acceptable.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in various real-world scenarios:
1. Finance and Budgeting:
- Interest rates: Calculating simple and compound interest on loans and investments.
- Discounts and sales: Determining the final price after a percentage discount.
- Taxes: Calculating sales tax, income tax, and other taxes.
- Profit margins: Assessing the profitability of a business.
- Investment returns: Evaluating the performance of investments.
2. Statistics and Data Analysis:
- Percentages in data representation: Charts and graphs often use percentages to show proportions within a dataset.
- Statistical significance: Percentages are used to express the likelihood of an event occurring.
- Population statistics: Demographics often use percentages to represent proportions of different groups.
3. Everyday Life:
- Tipping: Calculating a tip in a restaurant.
- Sales and discounts: Understanding discounts offered on products.
- Cooking: Scaling recipes up or down based on percentages.
- Surveys and polls: Interpreting the results of surveys and polls expressed as percentages.
Expanding the Concept: Solving Similar Problems
The principles used to solve "What percent of 7 is 3?" can be applied to a variety of similar problems. For example:
- What percent of 15 is 5? Using the formula: (5/15) * 100 = 33.33%
- What percent of 20 is 8? Using the formula: (8/20) * 100 = 40%
- 12 is what percent of 48? Using the formula: (12/48) * 100 = 25%
By understanding the fundamental concepts and methods outlined above, you can confidently tackle a wide range of percentage problems.
Advanced Percentage Calculations
While the examples above deal with relatively straightforward percentage calculations, more complex scenarios exist. These might involve:
- Calculating percentage change: Determining the increase or decrease in a quantity over time. For example, if sales increased from 100 units to 120 units, the percentage increase is ((120-100)/100) * 100 = 20%.
- Calculating percentage points: This refers to the difference between two percentages. For example, if interest rates increased from 2% to 5%, the increase is 3 percentage points, not 150%.
- Compound percentages: This involves calculating percentages on a growing base. For example, compound interest calculations involve applying interest to the principal plus accumulated interest.
Conclusion
The question "What percent of 7 is 3?" serves as a springboard for understanding the broader concept of percentage calculations. This article has explored different methods for solving this type of problem, highlighting the importance of proportions, the percentage formula, and the relationship between fractions, decimals, and percentages. Furthermore, we've explored the wide-ranging applications of percentage calculations in various aspects of life, from finance to everyday decision-making. Mastering percentage calculations empowers you to navigate numerical information more effectively and confidently in both professional and personal settings. Remember to choose the method that you find most comfortable and efficient, and always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
5 7 Divided By 1 3
May 12, 2025
-
Cuanto Es 50 Millones De Pesos
May 12, 2025
-
5 8 2 5 As A Fraction
May 12, 2025
-
Cuanto Es 71 Fahrenheit En Centigrados
May 12, 2025
-
How Many Quarts Are Equal To 17 Gallons
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 7 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.