Whats 4 To The Power Of 4
Treneri
May 14, 2025 · 6 min read
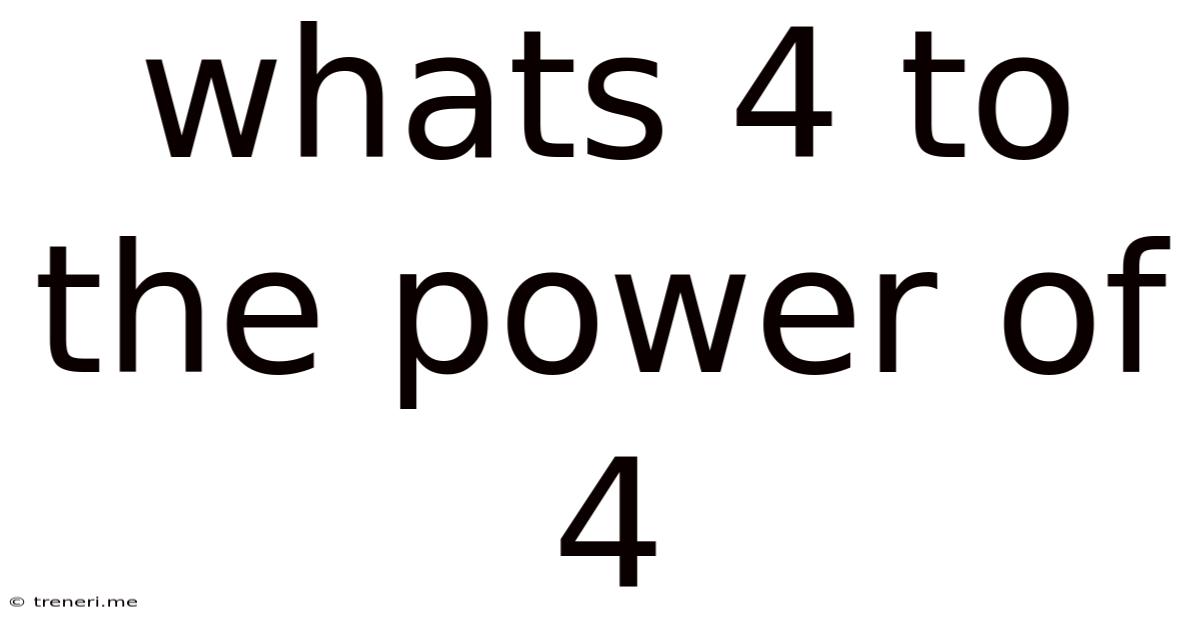
Table of Contents
What's 4 to the Power of 4? Unpacking Exponents and Their Applications
What's 4 to the power of 4? The answer, simply put, is 256. But this seemingly straightforward mathematical problem opens a door to a fascinating world of exponents, their properties, and their widespread applications across various fields. This article will delve deep into the concept of exponentiation, exploring not only the calculation of 4<sup>4</sup> but also the broader implications and real-world uses of this fundamental mathematical operation.
Understanding Exponents: A Foundation in Mathematics
Before we delve deeper into the specifics of 4<sup>4</sup>, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, b represents the base, and n represents the exponent. This expression is read as "b raised to the power of n."
For instance:
- 2<sup>3</sup> = 2 × 2 × 2 = 8 (2 is multiplied by itself 3 times)
- 5<sup>2</sup> = 5 × 5 = 25 (5 is multiplied by itself 2 times)
- 10<sup>1</sup> = 10 (10 is multiplied by itself 1 time, or simply 10)
- 7<sup>0</sup> = 1 (Any non-zero number raised to the power of 0 is always 1)
These examples highlight the fundamental principle of exponents: repeated multiplication.
Calculating 4 to the Power of 4 (4<sup>4</sup>)
Now, let's tackle the central question: What is 4 to the power of 4? Using the definition of exponents, we can calculate this as follows:
4<sup>4</sup> = 4 × 4 × 4 × 4 = 256
Therefore, 4 raised to the power of 4 equals 256. This seemingly simple calculation has far-reaching implications in various fields.
Beyond the Calculation: The Significance of Exponents
The significance of exponents extends far beyond simple calculations like 4<sup>4</sup>. Understanding exponents is crucial for grasping various mathematical concepts and their applications in the real world. Here are some key areas where exponents play a vital role:
1. Scientific Notation and Extremely Large or Small Numbers
Exponents are indispensable when dealing with extremely large or small numbers, commonly encountered in science and engineering. Scientific notation uses exponents to express these numbers concisely. For example, the speed of light is approximately 3 x 10<sup>8</sup> meters per second. This notation makes it far easier to handle such large numbers than writing out 300,000,000.
2. Compound Interest and Financial Growth
Exponents are at the heart of compound interest calculations. Compound interest involves earning interest not only on the principal amount but also on accumulated interest. The formula for compound interest uses exponents to model the growth over time. Understanding this is essential for anyone managing investments or loans.
3. Exponential Growth and Decay
Many phenomena in nature and science exhibit exponential growth or decay. Population growth, radioactive decay, and the spread of diseases can often be modeled using exponential functions. These functions rely heavily on exponents to depict the rapid increase or decrease over time. Understanding these models is critical for predicting future trends and making informed decisions.
4. Computer Science and Data Storage
In computer science, exponents are crucial for understanding data storage capacity. The prefixes like kilo (10<sup>3</sup>), mega (10<sup>6</sup>), giga (10<sup>9</sup>), and tera (10<sup>12</sup>) are all based on powers of 10. These prefixes help represent the vast amounts of data handled by computers and storage devices. Similarly, binary numbers (base 2) and their powers play a crucial role in digital systems.
5. Probability and Statistics
Exponents frequently appear in probability and statistics calculations, particularly in scenarios involving repeated independent events. For instance, calculating the probability of getting heads five times in a row when flipping a coin involves exponents in the calculation.
Practical Applications of 4<sup>4</sup> and Related Concepts
While 4<sup>4</sup> = 256 might seem like an isolated calculation, it's a specific instance of a broader mathematical concept with real-world relevance. Understanding this calculation and its underlying principles enables us to solve more complex problems. For example:
1. Data Organization and Grid Systems
Imagine a square grid with 4 rows and 4 columns. The total number of cells in this grid is 4 × 4 = 16. However, if we consider a 4 x 4 x 4 cube, the number of cubic cells would be 4<sup>3</sup> = 64. Extending this to a 4-dimensional hypercube, we would have 4<sup>4</sup> = 256 units. This concept is relevant in various fields like data storage, network topology, and computer graphics.
2. Combinatorics and Permutations
In combinatorics, the number of ways to arrange or choose items often involves exponents. For example, if you have 4 different colored balls and you want to arrange them in a row, there are 4! (4 factorial) = 4 × 3 × 2 × 1 = 24 possible arrangements. However, if you have 4 different colored balls and 4 different colored boxes, the number of ways to place the balls into the boxes is 4<sup>4</sup> = 256.
3. Geometric Progressions
A geometric progression is a sequence where each term is found by multiplying the previous term by a constant. The sum of a geometric progression can be calculated using a formula that involves exponents. Understanding this is important in financial mathematics, physics, and other areas.
Expanding on Exponents: Further Exploration
The concept of exponents can be further expanded into more complex areas, including:
1. Fractional Exponents and Roots
Fractional exponents represent roots. For instance, 4<sup>1/2</sup> is the square root of 4, which is 2. Understanding fractional exponents allows us to solve equations involving roots and to generalize the concept of exponentiation.
2. Negative Exponents
Negative exponents represent reciprocals. For instance, 4<sup>-1</sup> = 1/4. Understanding negative exponents allows us to extend the concept of exponentiation to negative numbers.
3. Complex Exponents
Exponents can even be complex numbers, leading to fascinating mathematical relationships explored in advanced calculus and complex analysis.
4. Logarithms
Logarithms are the inverse of exponents. If b<sup>n</sup> = x, then log<sub>b</sub>(x) = n. Logarithms are crucial in various scientific and engineering applications, including measuring the intensity of earthquakes (Richter scale) and the acidity of solutions (pH scale).
Conclusion: The Ubiquity of Exponents
The simple question "What's 4 to the power of 4?" leads us to a comprehensive exploration of exponents, a fundamental mathematical concept with vast applications in numerous fields. From scientific notation and compound interest to computer science and probability, exponents play a crucial role in modeling and understanding various phenomena. Understanding exponents, their properties, and their diverse applications is essential for anyone pursuing studies or careers in STEM fields or any area involving quantitative analysis. The seemingly simple calculation of 4<sup>4</sup> = 256 is therefore a gateway to a much larger and fascinating mathematical universe.
Latest Posts
Latest Posts
-
How Many Years Is 109 Months
May 14, 2025
-
What Is The Gcf Of 52 And 78
May 14, 2025
-
Is 8 10 Equivalent To 4 5
May 14, 2025
-
How Much More Time Until 12 Pm
May 14, 2025
-
1984 A 2024 Cuantos Anos Son
May 14, 2025
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.