Which Fraction Is Equivalent To 6/8
Treneri
May 09, 2025 · 6 min read
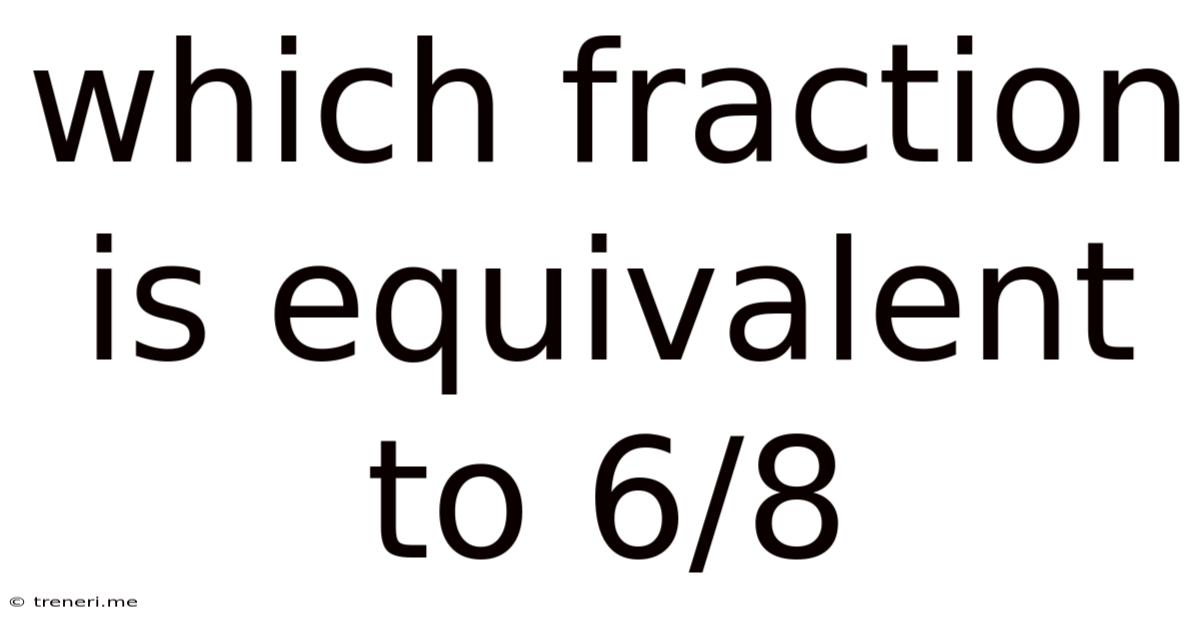
Table of Contents
Which Fraction is Equivalent to 6/8? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially for younger learners. However, understanding the underlying principles of equivalent fractions is crucial for mastering more advanced mathematical concepts. This comprehensive guide will not only answer the question "Which fraction is equivalent to 6/8?" but will also delve into the mechanics of finding equivalent fractions, exploring various methods and providing ample practice problems. We'll also discuss the real-world applications of this fundamental mathematical concept.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they appear different. Imagine slicing a pizza. If you cut it into 8 slices and take 6, you have 6/8 of the pizza. Now, imagine cutting the same pizza into 4 slices. You'd only need to take 3 slices to have the same amount of pizza—3/4. Both 6/8 and 3/4 represent the same portion of the whole pizza. They are equivalent fractions.
The key principle is that equivalent fractions are created by multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process maintains the ratio between the numerator and the denominator, ensuring the fraction represents the same value.
Finding Equivalent Fractions: Methods and Examples
Several methods can help you find equivalent fractions. Let's explore the most common ones:
1. Multiplying the Numerator and Denominator
This is the most straightforward method. To find an equivalent fraction, multiply both the numerator and the denominator of the original fraction by the same whole number (greater than 1).
Example: Let's find an equivalent fraction for 6/8. We can multiply both the numerator and the denominator by 2:
(6 x 2) / (8 x 2) = 12/16
Therefore, 12/16 is an equivalent fraction to 6/8. We can continue this process using different multipliers:
- (6 x 3) / (8 x 3) = 18/24
- (6 x 4) / (8 x 4) = 24/32
- and so on...
All these fractions (12/16, 18/24, 24/32, etc.) represent the same value as 6/8.
2. Dividing the Numerator and Denominator
This method is used to simplify fractions, finding the simplest form of the fraction. We divide both the numerator and the denominator by their greatest common divisor (GCD).
Example: Let's simplify 6/8. The GCD of 6 and 8 is 2. Dividing both by 2:
6 ÷ 2 / 8 ÷ 2 = 3/4
Therefore, the simplest form of 6/8 is 3/4. This is the most simplified equivalent fraction for 6/8. It's important to note that while 3/4 is the simplest form, there are infinitely many other equivalent fractions.
3. Using Visual Aids
Visual aids like fraction bars, circles, or diagrams can help visualize equivalent fractions. Dividing a shape into parts and shading a portion helps understand the concept of equivalent fractions concretely.
Example: Imagine a rectangle divided into 8 equal parts. Shade 6 of them. Now, imagine the same rectangle divided into 4 equal parts. You will see that shading 3 parts in the second rectangle represents the same area as shading 6 parts in the first rectangle. This visually confirms that 6/8 is equivalent to 3/4.
Answering the Question: Which Fraction is Equivalent to 6/8?
The question "Which fraction is equivalent to 6/8?" doesn't have a single answer. There are infinitely many equivalent fractions. However, the most common and often sought-after equivalent fraction is its simplest form, which is 3/4. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 2.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various real-world applications:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. Understanding equivalent fractions helps accurately scale recipes up or down. For example, if a recipe calls for 1/2 cup of sugar and you want to double the recipe, you need to know that 1/2 is equivalent to 2/4 or 3/6.
-
Measurement: Converting between different units of measurement, like inches to feet or centimeters to meters, involves using equivalent fractions.
-
Construction and Engineering: Accurate measurements and calculations are critical in construction and engineering projects. Working with fractions and understanding equivalent fractions ensures precise execution of plans.
-
Financial Calculations: Equivalent fractions are crucial in finance for understanding proportions, ratios, and percentages. For instance, calculating interest rates or determining a share of profits necessitates a solid grasp of equivalent fractions.
-
Data Analysis and Statistics: When working with proportions or percentages in data analysis, understanding equivalent fractions enables easier comparison and interpretation of results.
-
Everyday Life: From dividing a pizza fairly amongst friends to understanding sales discounts expressed as fractions, equivalent fractions are encountered in numerous everyday situations.
Practice Problems
Let's solidify our understanding with some practice problems:
-
Find three equivalent fractions for 2/5. (Hint: Use the multiplication method)
-
Simplify the fraction 15/25 to its simplest form. (Hint: Use the division method)
-
Is 16/24 equivalent to 2/3? (Hint: Simplify both fractions to their simplest form)
-
A recipe calls for 1/4 cup of milk. If you want to triple the recipe, how much milk will you need? (Hint: find an equivalent fraction of 1/4 that is easily multiplied by 3)
-
Draw a diagram to show that 2/6 is equivalent to 1/3. (Hint: use shapes divided into equal parts)
Solutions:
- 6/15, 8/20, 10/25 (Many other answers are possible)
- 3/5
- Yes, both simplify to 2/3
- 3/4 cup
- (Requires a visual diagram – draw a rectangle divided into 6 equal parts, shade 2. Then draw another rectangle divided into 3 equal parts, shade 1. Both show the same proportion.)
Conclusion
This in-depth exploration of equivalent fractions not only answers the initial question but also provides a robust understanding of the underlying principles and practical applications. Mastering equivalent fractions is a cornerstone of mathematical proficiency and has far-reaching implications across various disciplines and everyday life. Remember to practice regularly, utilize different methods, and visualize the concepts using diagrams or other aids to enhance your comprehension and build confidence in working with fractions. The more you practice, the easier it will become, and you’ll quickly develop a strong intuition for working with equivalent fractions. Remember, there are infinitely many equivalent fractions for any given fraction—find the one that's most useful for your specific task!
Latest Posts
Latest Posts
-
How To Find The Center Of A Sphere
May 09, 2025
-
4 Is 20 Percent Of What Number
May 09, 2025
-
Cuanto Falta Para El 23 De Agosto
May 09, 2025
-
Calories Burned On Stairmaster Level 5
May 09, 2025
-
What Fraction Is Equivalent To 6 10
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 6/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.