16 Is What Percent Of 32
Treneri
May 13, 2025 · 5 min read
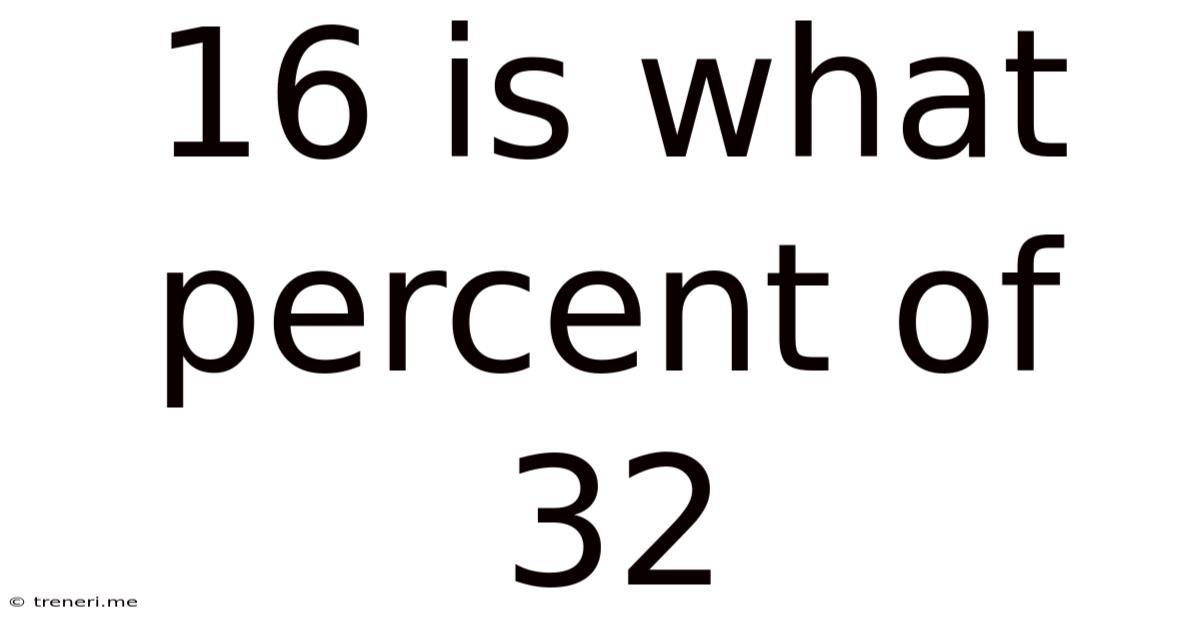
Table of Contents
16 is What Percent of 32: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into the seemingly simple question, "16 is what percent of 32?", providing a comprehensive explanation of the calculation, exploring different methods, and expanding on the broader applications of percentage calculations. We will cover everything from the basic formula to advanced techniques, ensuring you gain a thorough grasp of this essential mathematical concept.
Understanding the Fundamentals of Percentages
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred," indicating a ratio of a number to 100. For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal.
Key Concepts:
- Part: This represents the specific portion of the whole that we are interested in. In our example, 16 is the part.
- Whole: This represents the total amount or the complete quantity. In our example, 32 is the whole.
- Percentage: This represents the proportion of the part to the whole, expressed as a percentage (%).
Calculating "16 is What Percent of 32?"
There are several ways to calculate what percentage 16 represents of 32. Let's explore the most common methods:
Method 1: Using the Basic Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
(16 / 32) * 100% = Percentage
Solving this equation:
(0.5) * 100% = 50%
Therefore, 16 is 50% of 32.
Method 2: Using Proportions
Another effective method involves setting up a proportion:
16/32 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
16 * 100 = 32 * x
1600 = 32x
x = 1600 / 32
x = 50
Therefore, 16 is 50% of 32.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction 16/32 into a decimal:
16 / 32 = 0.5
Then, multiply the decimal by 100% to express it as a percentage:
0.5 * 100% = 50%
This confirms that 16 is 50% of 32.
Expanding on Percentage Calculations: Real-World Applications
Understanding percentage calculations extends far beyond simple arithmetic problems. Let's explore some real-world applications:
1. Financial Calculations:
- Discounts: Imagine a $40 item is discounted by 25%. The discount amount is (25/100) * $40 = $10. The final price would be $40 - $10 = $30.
- Taxes: If a sales tax is 8%, and you buy an item for $100, the tax amount would be (8/100) * $100 = $8. The total cost would be $100 + $8 = $108.
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans involves percentage calculations.
- Investment Returns: Tracking the performance of investments requires calculating percentage returns.
2. Data Analysis and Statistics:
- Percentages in Charts and Graphs: Visualizing data effectively often involves representing data as percentages in pie charts, bar graphs, and other visual aids.
- Statistical Analysis: Many statistical measures, like percentages, are expressed as percentages to easily understand the distribution and comparison of data sets.
- Surveys and Polls: Results from surveys and polls are frequently presented as percentages to convey the proportion of respondents holding a particular viewpoint.
3. Everyday Life:
- Tip Calculation: Determining the appropriate tip in a restaurant often involves calculating a percentage of the bill.
- Recipe Adjustments: If a recipe needs to be scaled up or down, percentage calculations are helpful in adjusting the ingredient quantities.
- Sales and Markdowns: Understanding percentage discounts helps in making informed purchasing decisions.
Advanced Percentage Calculations
While the example of "16 is what percent of 32" is relatively straightforward, percentage calculations can become more complex. Let's briefly explore some scenarios:
1. Finding the Whole When the Percentage and Part Are Known:
If you know that 20% of a certain number is 10, you can find the whole number using the formula:
Whole = (Part / Percentage) * 100
In this example:
Whole = (10 / 20) * 100 = 50
2. Finding the Part When the Percentage and Whole Are Known:
If you know that 30% of 200 is a certain number, you can find the part using the formula:
Part = (Percentage / 100) * Whole
In this example:
Part = (30 / 100) * 200 = 60
3. Percentage Change:
Calculating percentage change (increase or decrease) involves comparing two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100%
This is crucial for analyzing trends and comparing data over time.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice percentage calculations, the more comfortable and proficient you will become.
- Understand the Formula: Make sure you thoroughly understand the basic percentage formula and its variations.
- Use a Calculator: For complex calculations, a calculator can save time and increase accuracy.
- Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, manageable steps.
- Check Your Work: Always check your work to ensure accuracy. You can use different methods to verify your results.
Conclusion: The Importance of Percentage Calculations in a Data-Driven World
Understanding percentages is crucial in navigating the modern world, brimming with data and information presented in percentage form. From personal finance to professional analysis, mastering percentage calculations empowers you to make informed decisions, interpret data effectively, and succeed in numerous aspects of life. While the question "16 is what percent of 32?" may seem simple, the underlying principles have wide-ranging applications and are essential for anyone aiming to develop strong numerical literacy. Remember to practice regularly, understand the underlying formulas, and you’ll become a percentage calculation expert in no time!
Latest Posts
Latest Posts
-
Cuantos Metros Es Una Hectarea De Terreno
May 13, 2025
-
What Percentage Of An Hour Is 50 Minutes
May 13, 2025
-
Greatest Common Factor Of 42 And 12
May 13, 2025
-
What Is 3 8 1 3 In Fraction Form
May 13, 2025
-
X 1 2 In Radical Form
May 13, 2025
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.