7 10 Divided By 1 5
Treneri
May 12, 2025 · 6 min read
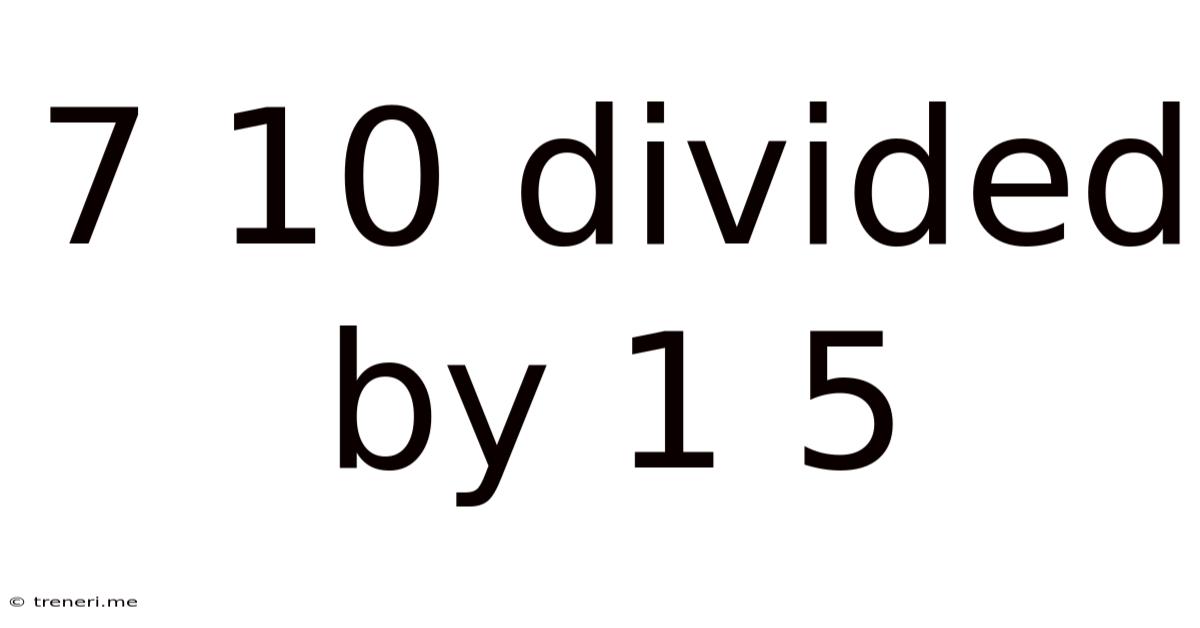
Table of Contents
Decoding the Division: A Deep Dive into 7.10 ÷ 1.5
The seemingly simple mathematical expression, 7.10 ÷ 1.5, often presents a stumbling block for many. While calculators readily provide the answer, understanding the underlying principles and exploring various methods of solution is crucial for building a strong foundation in mathematics and problem-solving. This article will not only solve 7.10 ÷ 1.5 but also delve into different approaches, highlighting their respective merits and applications. We'll also examine the broader context of decimal division, providing you with a comprehensive understanding that extends far beyond this specific problem.
Understanding Decimal Division
Before tackling the problem directly, let's establish a clear understanding of decimal division. Decimal numbers, characterized by the presence of a decimal point, represent fractions or parts of a whole. Dividing decimal numbers involves determining how many times one decimal number (the divisor) fits into another (the dividend). The process is essentially an extension of whole number division, requiring careful consideration of the decimal point's placement.
Method 1: Long Division
Long division remains a fundamental method for tackling decimal division. While it might seem tedious initially, mastering long division builds a strong intuition for the underlying mathematical processes. Here's how to solve 7.10 ÷ 1.5 using long division:
-
Adjust the Divisor: To simplify the process, we can remove the decimal point from the divisor (1.5) by multiplying it by 10. We must then perform the same operation on the dividend (7.10). This yields: 71 ÷ 15.
-
Initiate Long Division: Set up the long division problem: 15 | 71
-
Divide: How many times does 15 go into 71? It goes in 4 times (15 x 4 = 60). Write "4" above the 1 in 71.
-
Subtract: Subtract 60 from 71, resulting in 11.
-
Bring Down: Bring down the next digit (which is a 0, implicitly understood in this case since 7.10 is the same as 7.1).
-
Divide Again: How many times does 15 go into 110? It goes in 7 times (15 x 7 = 105). Write "7" above the 0.
-
Subtract Again: Subtract 105 from 110, resulting in 5.
-
Interpret the Remainder: The remainder, 5, indicates that 15 doesn't divide evenly into 71. We can express this remainder as a fraction (5/15) or continue the long division process by adding zeros and continuing the division. Simplifying the fraction, we get 1/3.
-
Final Answer: Therefore, 7.10 ÷ 1.5 = 4.7 + 1/3, or approximately 4.733.
Method 2: Converting to Fractions
Another robust method involves converting the decimals into fractions and performing the division.
-
Convert to Fractions: 7.10 can be written as 71/10, and 1.5 can be written as 3/2.
-
Invert and Multiply: Division by a fraction is the same as multiplying by its reciprocal. Therefore, the problem becomes (71/10) x (2/3).
-
Simplify: Multiply the numerators and the denominators: (71 x 2) / (10 x 3) = 142/30.
-
Simplify Further: Both the numerator and the denominator are divisible by 2, simplifying the fraction to 71/15.
-
Convert to Decimal: Now we perform the division: 71 ÷ 15 = 4 with a remainder of 11. This gives us 4 and 11/15. Converting 11/15 to decimal we get approximately 0.733.
-
Final Answer: Therefore, 7.10 ÷ 1.5 = 4.733.
Method 3: Using a Calculator
While not as insightful as the previous methods, using a calculator provides a quick and efficient solution, especially for more complex decimal divisions. Simply input 7.10 ÷ 1.5 and the calculator will instantly return the result: 4.733333... Note that this answer is often displayed as a recurring decimal.
Exploring the Significance of the Result
The result, approximately 4.733, tells us that 1.5 fits into 7.10 approximately 4.733 times. This seemingly simple statement has practical applications in numerous fields:
-
Engineering: Calculating material quantities, determining dimensions, and many other design processes heavily rely on accurate decimal division.
-
Finance: Dividing expenses or profits, calculating interest rates, and performing various financial analyses involve working with decimal numbers.
-
Science: In scientific experiments and data analysis, precise calculations with decimals are crucial for drawing accurate conclusions.
Beyond the Numbers: Building Mathematical Intuition
While the solution to 7.10 ÷ 1.5 is straightforward, the process of arriving at the solution reinforces important mathematical concepts. Understanding different methods not only improves calculation skills but also develops a deeper understanding of numbers and their relationships. This intuitive grasp of mathematics is invaluable for solving more complex problems and tackling challenges that go beyond simple arithmetic.
Practical Applications and Real-World Scenarios
Let’s consider some practical scenarios where this type of calculation would be necessary:
-
Recipe Scaling: Imagine you have a recipe that calls for 1.5 cups of flour and you want to triple the recipe. You'd need to calculate 1.5 x 3 = 4.5 cups. Conversely, if you only had 7.1 cups of flour, you could calculate how many times you could make the recipe (7.1 ÷ 1.5 ≈ 4.73), indicating you could make almost 5 smaller batches.
-
Construction: If you're cutting a 7.1-meter long piece of wood into sections of 1.5 meters each, you would use this division to determine you can get approximately 4 full-length sections and a smaller piece.
-
Fuel Efficiency: Let’s say your car consumes 1.5 liters of fuel per kilometer, and you have 7.1 liters in the tank. This calculation helps determine the approximate distance you can travel before refilling (7.1 ÷ 1.5 ≈ 4.73 kilometers).
Addressing Potential Errors and Common Mistakes
When working with decimal division, several common mistakes can lead to inaccurate results:
-
Misplacing the Decimal Point: Careful attention must be paid to the decimal point's placement during the calculation process. A misplaced decimal point can significantly alter the result.
-
Incorrect Rounding: When rounding off the result, it's crucial to maintain the necessary level of accuracy depending on the context of the problem. Rounding too drastically can lead to significant errors.
-
Ignoring Remainders: Failing to account for the remainder can lead to an incomplete or inaccurate result, particularly in situations where precision is critical.
Conclusion: Mastering Decimal Division for a Stronger Foundation
This in-depth exploration of 7.10 ÷ 1.5 highlights the importance of understanding decimal division beyond simply obtaining a numerical answer. Mastering various approaches—long division, fraction conversion, and calculator usage—builds a strong mathematical foundation and enhances problem-solving skills applicable across various domains. By understanding the underlying principles and being mindful of potential pitfalls, you can confidently tackle decimal division problems and apply this knowledge to numerous real-world scenarios. Remember to always double-check your work and consider the context of the problem to ensure accuracy and meaningful interpretation of the results. The seemingly simple act of dividing 7.10 by 1.5 opens doors to a much broader understanding of mathematics and its practical applications.
Latest Posts
Latest Posts
-
681 Rounded To The Nearest Ten
May 12, 2025
-
What Percent Of 8 Is 1
May 12, 2025
-
What Percent Is 16 Out Of 30
May 12, 2025
-
What Is The Total Surface Area Of This Rectangular Pyramid
May 12, 2025
-
What Angle Is A 4 12 Pitch Roof
May 12, 2025
Related Post
Thank you for visiting our website which covers about 7 10 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.