Gcf Of 16 32 And 72
Treneri
May 13, 2025 · 5 min read
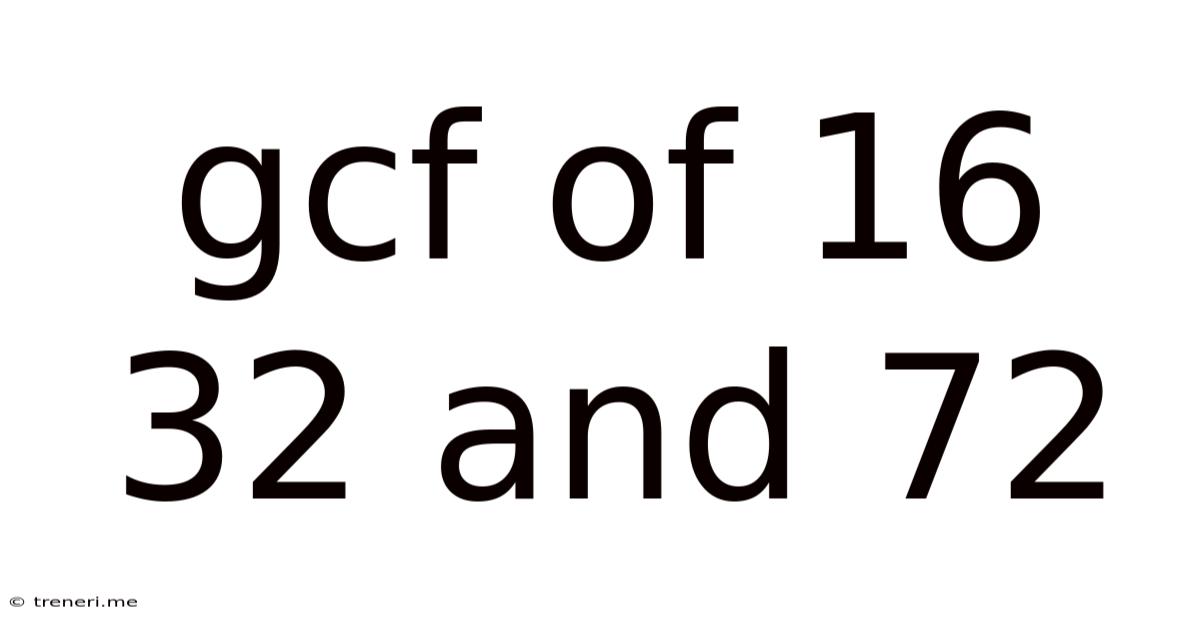
Table of Contents
Finding the Greatest Common Factor (GCF) of 16, 32, and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will delve into the process of determining the GCF of 16, 32, and 72, exploring various methods and illustrating their practical use. We'll also examine the significance of GCF in different mathematical contexts.
Understanding the Greatest Common Factor (GCF)
Before we embark on calculating the GCF of 16, 32, and 72, let's establish a clear understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of all the given numbers.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
Methods for Finding the GCF
Several methods exist for determining the GCF of a set of numbers. We'll explore the most common and efficient approaches, applying them to find the GCF of 16, 32, and 72.
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to all.
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 32: 1, 2, 4, 8, 16, 32
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
By comparing the lists, we can see that the common factors of 16, 32, and 72 are 1, 2, 4, and 8. The greatest of these common factors is 8. Therefore, the GCF(16, 32, 72) = 8.
This method is straightforward for smaller numbers but can become cumbersome and time-consuming as the numbers grow larger.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2<sup>4</sup>
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2<sup>3</sup> x 3<sup>2</sup>
To find the GCF using prime factorization, we identify the common prime factors and take the lowest power of each. In this case, the only common prime factor is 2, and its lowest power is 2<sup>3</sup> = 8. Therefore, the GCF(16, 32, 72) = 8.
This method is generally more efficient than listing factors, especially for larger numbers, as it systematically breaks down the numbers into their fundamental components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by applying it iteratively. The algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 16 and 32 first:
- 32 = 16 x 2 + 0 (The remainder is 0, so the GCF(16, 32) = 16)
Now let's find the GCF of 16 and 72:
- 72 = 16 x 4 + 8
- 16 = 8 x 2 + 0 (The remainder is 0, so the GCF(16, 72) = 8)
Therefore, the GCF(16, 32, 72) = 8.
The Euclidean algorithm is particularly useful for larger numbers because it avoids the need for full prime factorization, making it computationally more efficient.
Applications of the GCF
The concept of the greatest common factor finds applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is crucial in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, the fraction 16/32 can be simplified to 1/2 by dividing both the numerator and denominator by their GCF, which is 16.
-
Algebraic Expressions: GCF is used to factor algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows us to factor out the common factor, simplifying the expression.
-
Geometry: GCF plays a role in solving geometric problems involving area and volume calculations. For example, when finding the dimensions of the largest square tile that can perfectly cover a rectangular floor, the GCF of the length and width of the floor determines the side length of the tile.
-
Number Theory: GCF is a fundamental concept in number theory, a branch of mathematics that studies the properties of integers. It forms the basis for various theorems and algorithms related to divisibility and prime numbers.
-
Computer Science: The Euclidean algorithm, used for calculating the GCF, is an important algorithm in computer science with applications in cryptography and other areas. Its efficiency makes it suitable for implementation in computer programs to solve GCF problems quickly.
Conclusion
Determining the greatest common factor is a valuable skill with numerous applications across different mathematical disciplines. We have explored three primary methods – listing factors, prime factorization, and the Euclidean algorithm – each offering its own advantages and suitability depending on the context and magnitude of the numbers involved. Understanding the GCF is essential for simplifying fractions, factoring algebraic expressions, and solving various problems in geometry and number theory. The efficiency and versatility of these methods make them indispensable tools in various mathematical and computational contexts. Mastering these techniques is crucial for building a strong foundation in mathematics and its applications. By understanding and applying these methods, one can confidently tackle problems involving the greatest common factor. The GCF of 16, 32, and 72, as demonstrated through multiple methods, is definitively 8.
Latest Posts
Latest Posts
-
How Many Ounces In 230 Grams
May 13, 2025
-
1 Bar Is How Many Psi
May 13, 2025
-
4 Out Of 13 As A Percentage
May 13, 2025
-
What Percent Of 27 Is 18
May 13, 2025
-
16 Pints Equals How Many Cups
May 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 32 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.