Gcf Of 36 60 And 84
Treneri
May 09, 2025 · 5 min read
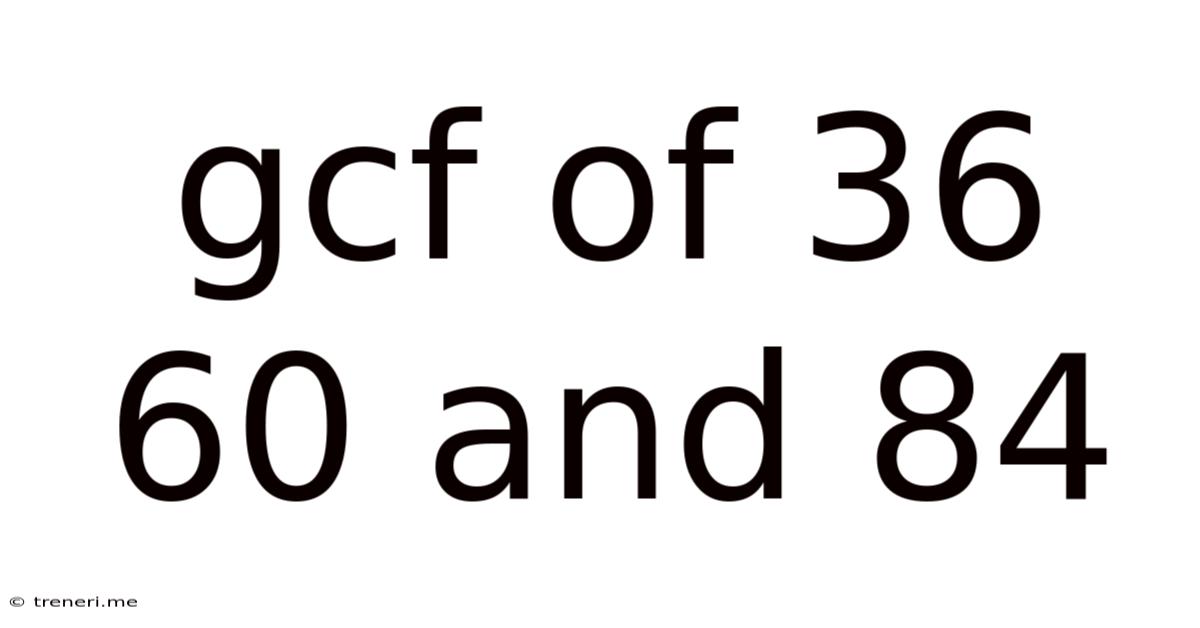
Table of Contents
Finding the Greatest Common Factor (GCF) of 36, 60, and 84: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with wide-ranging applications. This article provides a thorough exploration of how to determine the GCF of 36, 60, and 84, covering multiple methods and explaining the underlying principles. We'll delve into prime factorization, the Euclidean algorithm, and the listing factors method, illustrating each with detailed examples and clarifying common misconceptions. By the end, you'll not only know the GCF of these specific numbers but also possess a solid understanding of how to calculate the GCF for any set of numbers.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It's a crucial concept in simplifying fractions, solving algebraic equations, and various other mathematical applications. Understanding how to find the GCF is a valuable skill for students and professionals alike.
Method 1: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Then, the GCF is found by identifying the common prime factors and multiplying them together.
Step 1: Prime Factorization of 36
36 = 2 x 2 x 3 x 3 = 2² x 3²
Step 2: Prime Factorization of 60
60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
Step 3: Prime Factorization of 84
84 = 2 x 2 x 3 x 7 = 2² x 3 x 7
Step 4: Identifying Common Factors
Comparing the prime factorizations, we see that all three numbers share two factors: 2 and 3. Note that we take the lowest power of each common factor. Since 2² appears in all three factorizations, we use that for our calculation. The common factors are 2² and 3¹.
Step 5: Calculating the GCF
Multiply the common factors together: 2² x 3 = 4 x 3 = 12
Therefore, the GCF of 36, 60, and 84 is 12.
This method is particularly useful for understanding the underlying structure of the numbers and their relationships. It provides a clear visual representation of the common factors.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. For multiple numbers, we find the GCF of the first two numbers, then the GCF of that result and the third number, and so on.
Step 1: Finding the GCF of 36 and 60
- 60 = 1 x 36 + 24
- 36 = 1 x 24 + 12
- 24 = 2 x 12 + 0
The remainder is 0, so the GCF of 36 and 60 is 12.
Step 2: Finding the GCF of 12 and 84
- 84 = 7 x 12 + 0
The remainder is 0, so the GCF of 12 and 84 is 12.
Therefore, the GCF of 36, 60, and 84 is 12.
The Euclidean algorithm is computationally efficient, especially for larger numbers where prime factorization can become cumbersome.
Method 3: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. While straightforward for smaller numbers, it becomes less efficient with larger numbers.
Step 1: Factors of 36
1, 2, 3, 4, 6, 9, 12, 18, 36
Step 2: Factors of 60
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Step 3: Factors of 84
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Step 4: Identifying Common Factors
Comparing the lists, the common factors are 1, 2, 3, 4, 6, and 12.
Step 5: Determining the GCF
The largest common factor is 12.
Therefore, the GCF of 36, 60, and 84 is 12. While this method is less efficient for larger numbers, its simplicity can be beneficial for understanding the concept of factors.
Applications of the GCF
The GCF has numerous practical applications across various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 36/60 can be simplified to 3/5 by dividing both the numerator and denominator by their GCF, which is 12.
-
Algebra: The GCF is essential in factoring algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and solving equations.
-
Geometry: The GCF is used in geometry problems involving dividing shapes into smaller, equal parts. For example, finding the largest square tile that can evenly cover a rectangular floor.
-
Measurement: The GCF helps in determining the largest common unit of measurement for different quantities.
-
Number Theory: The GCF plays a critical role in various number theory concepts, such as modular arithmetic and Diophantine equations.
Conclusion: Mastering GCF Calculations
Determining the greatest common factor is a crucial skill in mathematics. This article has explored three effective methods—prime factorization, the Euclidean algorithm, and listing factors—for calculating the GCF, demonstrating each with the example of 36, 60, and 84. Understanding these methods equips you with the tools to find the GCF of any set of numbers, regardless of their size. Remember to choose the method that best suits the numbers and your comfort level. Whether you prefer the visual clarity of prime factorization, the efficiency of the Euclidean algorithm, or the straightforward approach of listing factors, mastering GCF calculations opens doors to a deeper understanding of mathematical concepts and their real-world applications. The GCF, seemingly a simple concept, underpins a multitude of important mathematical operations and problem-solving strategies.
Latest Posts
Latest Posts
-
Canine Pregnancy Calendar Day By Day
May 10, 2025
-
How To Measure Weight Of Gold
May 10, 2025
-
Find What Percent Of 5 Is 2
May 10, 2025
-
Tax And License Fees Calculator California
May 10, 2025
-
1 12 Of 1 3 Is What Fraction
May 10, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 36 60 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.