What Is 10 Percent Of 30000
Treneri
Apr 06, 2025 · 5 min read
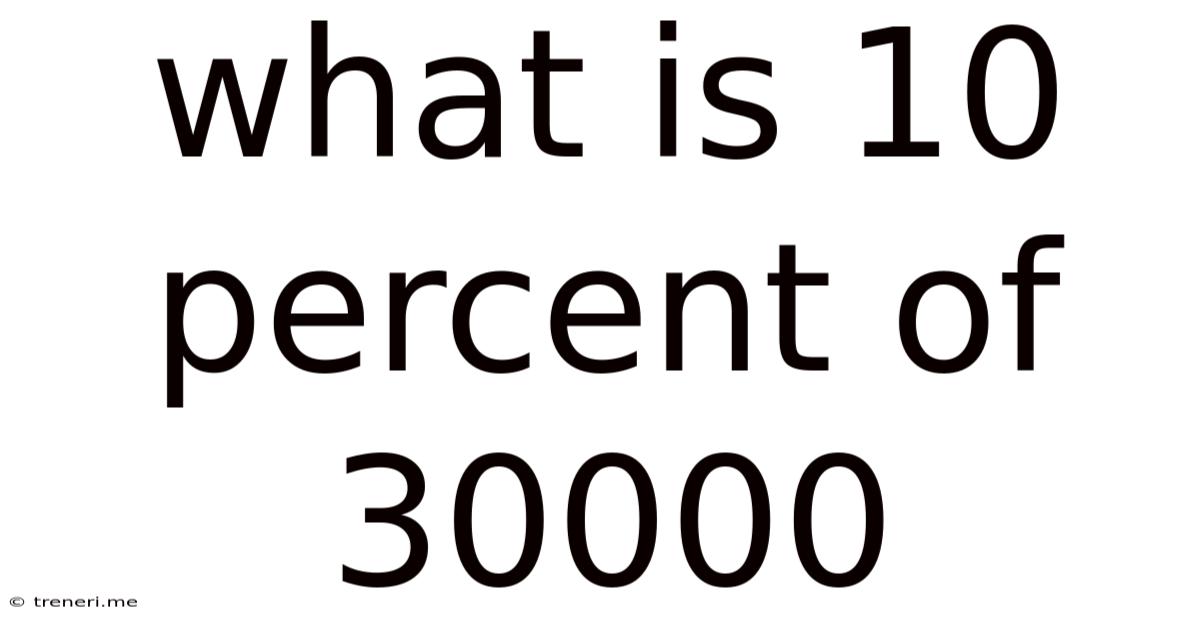
Table of Contents
What is 10 Percent of 30,000? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to calculate percentages accurately and efficiently is crucial for making informed decisions and navigating the numerical world effectively. This article will comprehensively explore the calculation of 10 percent of 30,000, offering multiple approaches, explaining the underlying concepts, and highlighting the widespread applications of percentage calculations in real-world scenarios.
Understanding Percentages: A Foundation for Calculation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Percentages are represented by the symbol "%". For example, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10.
Understanding this fundamental concept is key to calculating percentages efficiently. Many methods exist, each offering a different approach depending on the context and available tools. Let's explore various ways to calculate 10% of 30,000.
Method 1: The Direct Calculation Method
This is the most straightforward method, directly applying the definition of a percentage. Since 10% represents 10/100, we can express the calculation as follows:
(10/100) * 30,000 = 3,000
This method clearly demonstrates that 10% of 30,000 is 3,000. It's a simple and easily understood calculation.
Method 2: Using Decimal Equivalents
Percentages can also be expressed as decimal equivalents. 10% is equivalent to 0.10. Therefore, the calculation becomes:
0.10 * 30,000 = 3,000
This method highlights the versatility of percentage representation and how easily decimal equivalents can streamline calculations, particularly when using calculators or spreadsheets.
Method 3: The Proportion Method
This method utilizes the concept of proportions. We can set up a proportion to solve for the unknown value (x), representing 10% of 30,000:
10/100 = x/30,000
To solve for x, we cross-multiply:
10 * 30,000 = 100 * x
300,000 = 100x
Dividing both sides by 100, we get:
x = 3,000
The proportion method demonstrates a more formal approach to percentage calculations, suitable for situations requiring a clear and demonstrable solution.
Method 4: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage button (often represented by "%"). Simply enter "30000 * 10 %" and the calculator will directly output 3,000. This method is efficient and minimizes the risk of manual calculation errors, making it ideal for quick computations.
Method 5: Mental Math Techniques
For 10%, a simple mental shortcut exists. To find 10% of any number, simply move the decimal point one place to the left. Therefore, 10% of 30,000 is 3,000. This method relies on understanding the relationship between percentages and decimal places and is useful for quick estimations and mental calculations.
Real-world Applications of Percentage Calculations: Beyond the Basics
Calculating percentages isn't just an academic exercise; it's a crucial skill with numerous real-world applications. Understanding these applications highlights the practical importance of mastering percentage calculations.
1. Financial Calculations:
- Discounts: Calculating discounts on purchases is a common application of percentages. A 10% discount on a $30,000 car, for instance, would result in a savings of $3,000.
- Taxes: Determining sales tax, income tax, or other taxes often involves percentage calculations.
- Interest: Calculating simple or compound interest on loans, investments, or savings accounts relies heavily on percentages.
- Profit Margins: Businesses use percentages to determine profit margins, which are calculated as a percentage of revenue.
- Investment Returns: Investors track investment returns as percentages to measure the growth or decline of their investments.
2. Statistics and Data Analysis:
- Data Representation: Percentages are frequently used to represent data in graphs, charts, and tables, making complex data easier to understand and interpret.
- Statistical Measures: Percentages are integral to many statistical measures, such as percentages, proportions, and rates.
- Survey Results: Survey results are often presented as percentages to represent the proportion of respondents who answered in a particular way.
3. Everyday Life:
- Tip Calculation: Calculating tips in restaurants usually involves determining a percentage of the total bill.
- Sales Commissions: Salespeople often earn commissions based on a percentage of their sales.
- Grade Calculation: Grading systems often use percentages to represent a student's performance in a course.
4. Scientific Applications:
- Experimental Results: Scientists use percentages to represent the results of experiments and studies, showing the proportion of successful outcomes or changes observed.
- Data Modeling: Percentages are often used in various types of mathematical modeling to simulate real-world phenomena.
Expanding Your Percentage Skills: Beyond 10%
While this article focuses on calculating 10% of 30,000, the principles discussed apply to calculating any percentage of any number. Mastering the fundamental methods explained here will equip you to handle a wide range of percentage calculations with confidence.
For example, if you need to calculate 25% of 30,000, you can use any of the methods outlined above, simply substituting 25/100 or 0.25 for 10/100 or 0.10. Similarly, you can apply these methods to calculate percentages of other numbers.
Conclusion: The Power of Percentage Understanding
The ability to calculate percentages accurately is a valuable life skill. Understanding the various methods available and their applications in diverse fields equips you to make informed decisions, analyze data effectively, and navigate the quantitative aspects of everyday life and professional endeavors. From simple budgeting to complex financial analyses, the ability to calculate percentages confidently is an asset in many areas of life. Therefore, mastering this skill is highly recommended. Remember that practice is key – the more you apply these methods, the more intuitive and effortless percentage calculations will become.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 36 And 64
May 10, 2025
-
Whats The Perfect Uv For Tanning
May 10, 2025
-
1 Out Of 12 Is What Percent
May 10, 2025
-
What Is The Quotient Of 18 1000
May 10, 2025
-
66 Out Of 80 As A Percentage
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 30000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.