What Is 3 Percent Of 150
Treneri
May 14, 2025 · 5 min read
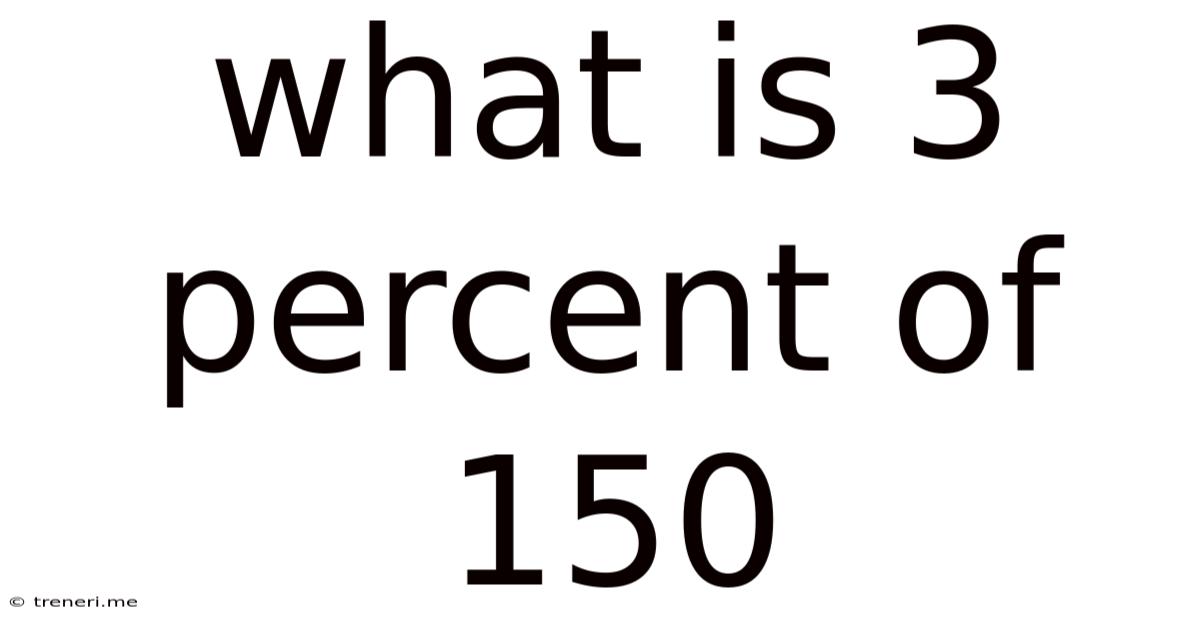
Table of Contents
What is 3 Percent of 150? A Deep Dive into Percentage Calculations
Finding 3 percent of 150 might seem like a simple task, a quick calculation easily done on a calculator. However, understanding the underlying principles of percentage calculations is crucial, not just for solving this specific problem but for a wide range of applications in everyday life and various professional fields. This comprehensive guide will not only provide the answer but will delve deep into the methodology, explore different approaches to solving percentage problems, and demonstrate the practical relevance of understanding percentages.
Understanding Percentages: The Foundation
Before we tackle the specific question, "What is 3 percent of 150?", let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." So, 3% means 3 out of 100, or 3/100. This fundamental concept is the cornerstone of all percentage calculations.
Key Terminology
- Percentage: A number or ratio expressed as a fraction of 100.
- Base: The whole amount or total value from which a percentage is calculated (in our case, 150).
- Rate: The percentage itself (in our case, 3%).
- Portion: The result of the percentage calculation, representing a part of the base (what we're trying to find).
Calculating 3 Percent of 150: Three Approaches
There are several ways to calculate 3% of 150. We'll explore three common methods:
Method 1: Using the Formula
The most straightforward method involves using the basic percentage formula:
Portion = (Rate/100) * Base
Substituting our values:
Portion = (3/100) * 150
Portion = 0.03 * 150
Portion = 4.5
Therefore, 3 percent of 150 is 4.5.
Method 2: Converting Percentage to Decimal
This method involves converting the percentage to its decimal equivalent before multiplying. To convert a percentage to a decimal, divide the percentage by 100 (or move the decimal point two places to the left).
3% = 3/100 = 0.03
Now, multiply the decimal equivalent by the base:
0.03 * 150 = 4.5
Again, we arrive at the same answer: 4.5
Method 3: Proportion Method
This method utilizes the concept of proportion. We can set up a proportion to solve for the unknown portion:
3/100 = x/150
To solve for x (the portion), we cross-multiply:
100x = 3 * 150
100x = 450
x = 450/100
x = 4.5
This method reinforces the underlying proportional relationship between percentages and the base value. It's particularly useful for understanding the concept and solving more complex percentage problems.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is not just an academic exercise. It's a vital skill applicable across numerous real-world scenarios:
1. Finance and Budgeting:
- Interest Calculations: Calculating simple or compound interest on loans, investments, or savings accounts heavily relies on percentage calculations.
- Discounts and Sales Tax: Determining the final price of an item after a discount or adding sales tax requires understanding how percentages affect the base price.
- Investment Returns: Tracking the performance of investments, whether stocks, bonds, or real estate, requires calculating percentage returns (gains or losses).
- Budgeting: Allocating funds for different budget categories involves calculating percentages of total income.
2. Data Analysis and Statistics:
- Calculating Percentages: Representing data using percentages provides a concise and easily understandable way to visualize proportions within a dataset. This is crucial in fields like market research, scientific studies, and economic analysis.
- Growth Rates: Analyzing growth rates in various metrics, such as population growth, economic growth, or sales growth, involves calculating percentage changes over time.
- Probability: Probability is often expressed as a percentage, offering a clear representation of the likelihood of an event occurring.
3. Everyday Life:
- Tip Calculation: Determining the appropriate tip amount in a restaurant often involves calculating a percentage of the total bill.
- Commission Calculations: Salespeople often earn a commission based on a percentage of their sales.
- Recipe Scaling: Adjusting ingredient quantities in a recipe based on the number of servings involves calculating percentages.
Advanced Percentage Problems and Solving Techniques
While finding 3% of 150 is relatively simple, more complex percentage problems require a deeper understanding and potentially different techniques.
1. Finding the Percentage Increase or Decrease:
This involves calculating the percentage change between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
For example, if a price increases from $100 to $120, the percentage increase is:
[(120 - 100) / 100] * 100 = 20%
2. Finding the Original Value:
Sometimes, you know the percentage and the final value but need to find the original value. This requires rearranging the percentage formula.
For example, if a value is increased by 10% to reach 110, the original value can be calculated as:
Original Value = 110 / (1 + 10/100) = 100
3. Dealing with Multiple Percentages:
Calculating successive percentages requires careful attention to the order of operations. For instance, a 10% increase followed by a 10% decrease does not result in the original value.
Conclusion: Mastering Percentage Calculations
The seemingly simple question, "What is 3 percent of 150?" opens the door to a world of percentage calculations with broad applicability. By understanding the fundamental principles, different calculation methods, and the numerous practical applications, you can confidently tackle various percentage problems in everyday life, academic pursuits, and professional endeavors. The ability to calculate percentages accurately and efficiently is an invaluable skill that contributes to sound decision-making and problem-solving in many contexts. Remember to practice regularly and explore different approaches to solidify your understanding and build your confidence in tackling even the most challenging percentage problems.
Latest Posts
Latest Posts
-
Least Common Multiple Of 4 6 And 7
May 14, 2025
-
How Many Weeks Are In Five Years
May 14, 2025
-
Greatest Common Factor Of 72 And 45
May 14, 2025
-
How Many Bags Of Salt For 10000 Gallon Pool
May 14, 2025
-
15 Is 80 Percent Of What Number
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.