What Is The Greatest Common Factor Of 81 And 54
Treneri
May 09, 2025 · 5 min read
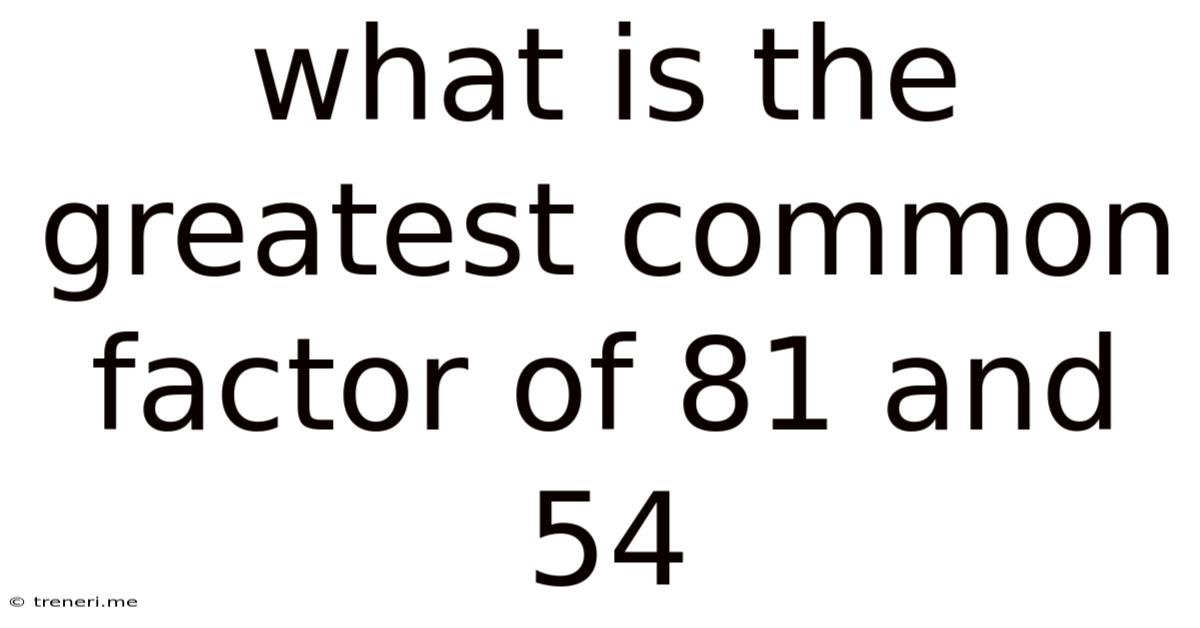
Table of Contents
What is the Greatest Common Factor (GCF) of 81 and 54? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications in various fields like cryptography, computer science, and even music theory. This article delves into the process of determining the GCF of 81 and 54, exploring multiple methods, and illuminating the underlying mathematical principles. We'll go beyond a simple answer, providing a comprehensive understanding that will empower you to tackle similar problems with confidence.
Understanding the Greatest Common Factor (GCF)
Before we jump into finding the GCF of 81 and 54, let's establish a clear understanding of what a GCF actually is. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest of these common factors is 6; therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 81 and 54. We list all the factors of each number and then identify the largest factor they have in common.
Factors of 81: 1, 3, 9, 27, 81
Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
By comparing the two lists, we can see that the common factors are 1, 3, 9, and 27. The greatest of these common factors is 27. Therefore, the GCF of 81 and 54 is 27.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Finding all factors of a large number can be time-consuming and prone to errors.
Method 2: Prime Factorization
This method is more systematic and efficient, especially for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 81:
81 = 3 x 27 = 3 x 3 x 9 = 3 x 3 x 3 x 3 = 3<sup>4</sup>
Prime factorization of 54:
54 = 2 x 27 = 2 x 3 x 9 = 2 x 3 x 3 x 3 = 2 x 3<sup>3</sup>
Now, we identify the common prime factors and their lowest powers. Both 81 and 54 share the prime factor 3. The lowest power of 3 present in both factorizations is 3<sup>3</sup> = 27. Therefore, the GCF of 81 and 54 is 27.
This method is more robust and less prone to errors, making it suitable for larger numbers where listing all factors would be impractical.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, regardless of their size. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 81 and 54:
- Start with the larger number (81) and the smaller number (54).
- Subtract the smaller number from the larger number: 81 - 54 = 27
- Replace the larger number with the result (27) and keep the smaller number (54). Now we have 54 and 27.
- Repeat the subtraction: 54 - 27 = 27
- The numbers are now equal (27 and 27), so the GCF is 27.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, especially for large numbers where prime factorization might be computationally expensive.
Applications of Finding the GCF
The seemingly simple task of finding the greatest common factor has far-reaching applications across various fields:
1. Simplifying Fractions:
GCF is crucial in simplifying fractions to their lowest terms. For example, the fraction 54/81 can be simplified by dividing both the numerator and the denominator by their GCF (27), resulting in the equivalent fraction 2/3.
2. Solving Problems in Algebra:
GCF plays a role in factoring algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and further algebraic manipulation.
3. Cryptography:
GCF is fundamental in many cryptographic algorithms, such as the RSA algorithm, which relies on the difficulty of finding the GCF of two very large numbers.
4. Computer Science:
GCF calculations are used in various computer science algorithms, including those related to data compression and scheduling.
5. Music Theory:
Interestingly, GCF finds its application in music theory. Determining the GCF of two note frequencies helps in identifying the intervals between notes and understanding harmonic relationships.
Conclusion: Mastering GCF Calculations
Finding the greatest common factor of two numbers is a fundamental mathematical operation with widespread practical applications. While the listing factors method is suitable for smaller numbers, the prime factorization and Euclidean algorithm offer more efficient and robust approaches for larger numbers. Understanding these methods empowers you to solve problems related to fraction simplification, algebraic manipulation, and even delve into the fascinating world of cryptography and music theory. The GCF of 81 and 54, as we've demonstrated through various methods, is definitively 27. Now you're equipped with the knowledge and tools to confidently tackle similar problems and appreciate the power of this seemingly simple concept. Remember, consistent practice is key to mastering these techniques. Try working through some examples on your own to solidify your understanding. Happy calculating!
Latest Posts
Latest Posts
-
Density Is Mass Per Unit Volume
May 11, 2025
-
What Is 7 Of 100 000
May 11, 2025
-
What Is The Gcf Of 96 And 84
May 11, 2025
-
90 Days From May 2 2024
May 11, 2025
-
Using Molarity To Find Solute Mass And Solution Volume
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 81 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.