Whats 5 To The Power Of 2
Treneri
May 09, 2025 · 5 min read
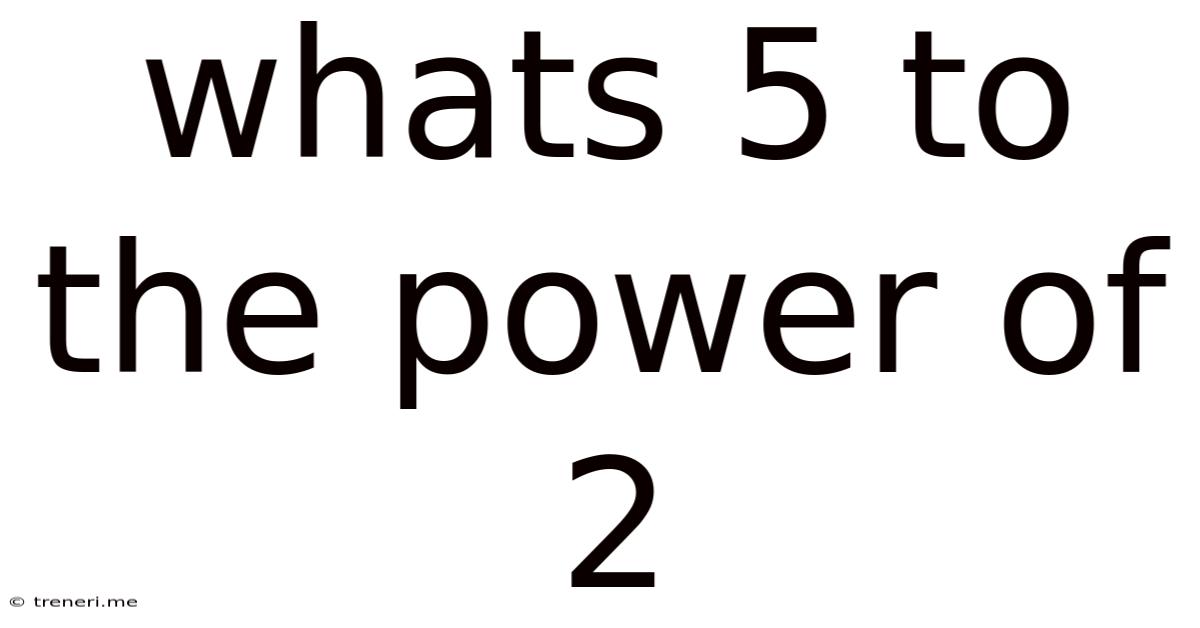
Table of Contents
What's 5 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What's 5 to the power of 2?" opens a door to a vast world of mathematical concepts with far-reaching applications in various fields. While the answer itself is straightforward (25), understanding the underlying principles of exponents unlocks a deeper comprehension of mathematics, computer science, finance, and even the natural world. This article will delve into the meaning of exponents, explore the specific case of 5², and then broaden the discussion to illustrate the significance of exponential functions in diverse contexts.
Understanding Exponents: The Fundamentals
Exponents, also known as powers or indices, represent repeated multiplication. The expression 5² (pronounced "5 to the power of 2" or "5 squared") signifies 5 multiplied by itself twice: 5 x 5 = 25. In general, the expression a<sup>b</sup> means that the base (a) is multiplied by itself b times. Here, a can be any number (positive, negative, or even a fraction), and b is the exponent, indicating the number of times the base is multiplied.
Key Components of an Exponential Expression
Let's break down the components of an exponential expression like 5²:
- Base (5): This is the number that is being multiplied repeatedly.
- Exponent (2): This is the number of times the base is multiplied by itself.
- Result (25): This is the outcome of the repeated multiplication.
Examples of Exponential Expressions
To solidify your understanding, let's consider some additional examples:
- 2³ = 2 x 2 x 2 = 8: 2 is the base, 3 is the exponent, and 8 is the result.
- 10¹ = 10: Any number raised to the power of 1 is itself.
- 7⁰ = 1: Any non-zero number raised to the power of 0 is always 1.
- 4⁻² = 1/(4²) = 1/16: A negative exponent signifies the reciprocal of the base raised to the positive power.
5²: A Closer Look
Returning to our initial question, 5² (5 to the power of 2) is simply 5 multiplied by itself twice: 5 x 5 = 25. This calculation is fundamental and serves as a building block for more complex mathematical operations. Understanding this basic calculation is crucial for grasping more advanced exponential concepts.
Beyond the Basics: Exponential Functions and Their Applications
The concept of exponents extends far beyond simple calculations like 5². Exponential functions, where the variable is in the exponent, are pervasive in various fields:
1. Exponential Growth and Decay
Exponential functions are vital for modeling phenomena exhibiting rapid growth or decay. Examples include:
- Population Growth: The growth of a population often follows an exponential pattern, particularly in environments with abundant resources.
- Compound Interest: The growth of an investment earning compound interest is another classic example of exponential growth. The interest earned in each period is added to the principal, leading to increasingly larger gains over time.
- Radioactive Decay: Radioactive substances decay at an exponential rate, with their mass decreasing over time. This is utilized in carbon dating to determine the age of ancient artifacts.
- Viral Spread: The spread of viral infections can often be modeled using exponential growth functions, particularly in the early stages of an outbreak.
2. Computer Science: Big O Notation
In computer science, Big O notation uses exponential functions to describe the time or space complexity of algorithms. An algorithm with exponential time complexity becomes incredibly slow as the input size increases. Understanding exponential growth is crucial for designing efficient and scalable algorithms.
3. Finance: Compound Interest Calculations
As mentioned earlier, compound interest is a prime example of exponential growth. Calculating future values of investments, understanding loan amortization schedules, and assessing the long-term impact of investment strategies all rely heavily on exponential functions. The formula for compound interest involves exponents, directly reflecting the compounding effect over time.
4. Physics and Engineering: Exponential Attenuation
In physics and engineering, exponential functions are used to model various phenomena involving attenuation or decay, such as:
- Signal Attenuation: The weakening of a signal as it travels through a medium, like an electrical signal in a cable or a light signal in an optical fiber.
- Heat Transfer: The rate of heat transfer can often be modeled using exponential decay functions.
5. Biology: Population Dynamics and Growth of Organisms
Exponential functions are widely used in modeling population dynamics in various biological contexts. They can describe the growth of bacterial colonies, the spread of diseases, or the growth of certain types of plants and animals.
6. Chemistry: Reaction Rates and Chemical Kinetics
In chemistry, exponential functions are used to model reaction rates and chemical kinetics. The rate at which reactants transform into products can sometimes be described by exponential functions, making it crucial for understanding chemical processes.
Expanding on Exponents: Beyond Integer Exponents
So far, we've primarily focused on integer exponents. However, the concept of exponents extends to rational and even irrational numbers:
Rational Exponents: Fractional Powers
A rational exponent, such as 5^(1/2), represents a root. 5^(1/2) is the square root of 5, approximately 2.236. Similarly, 5^(1/3) is the cube root of 5, and so on. Rational exponents combine roots and powers: for example, 5^(3/2) is equivalent to (√5)³.
Irrational Exponents: e and Natural Logarithms
Irrational exponents, like 5<sup>π</sup>, involve numbers that cannot be expressed as fractions. These are typically calculated using logarithms and numerical methods. The number e (Euler's number, approximately 2.718), is a fundamental constant in mathematics, and exponential functions with base e are ubiquitous in calculus and modeling continuous growth or decay processes. Natural logarithms (ln) are logarithms with base e, playing a crucial role in solving exponential equations and analyzing exponential growth/decay processes.
Conclusion: The Enduring Significance of Exponents
While the answer to "What's 5 to the power of 2?" is simply 25, the journey to understand the underlying principles of exponents unveils a rich mathematical landscape. The concept of exponents permeates various scientific and practical disciplines, allowing us to model complex phenomena, analyze data, and solve a wide array of problems. From compound interest calculations to the modeling of population growth, from algorithm analysis in computer science to the description of radioactive decay, the power of exponents continues to shape our understanding of the world around us. Mastering this fundamental concept is a cornerstone for further exploration in mathematics and its countless applications.
Latest Posts
Latest Posts
-
What Fraction Is Equal To 2 5
May 10, 2025
-
Cuanto Es 5 Onzas En Ml
May 10, 2025
-
01 To The Power Of 30
May 10, 2025
-
Cuanto Es 100 Dias En Meses
May 10, 2025
-
How Many Grams Equal A Half Ounce
May 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.