Which Fraction Is Equivalent To 2/8
Treneri
May 10, 2025 · 5 min read
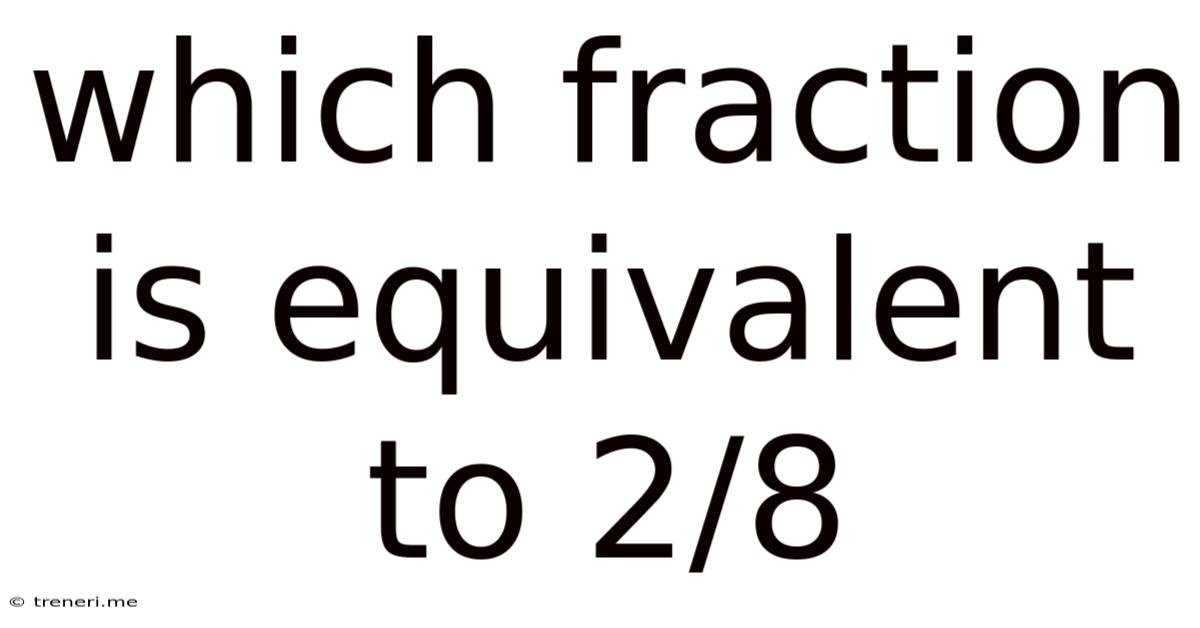
Table of Contents
Which Fraction is Equivalent to 2/8? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially when dealing with fractions like 2/8. However, understanding the underlying principles behind equivalent fractions is crucial for mastering more complex mathematical concepts. This comprehensive guide will not only answer the question "Which fraction is equivalent to 2/8?" but also explore the broader concept of equivalence, providing you with the tools and understanding to tackle similar problems with confidence.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or part of a whole, even though they look different. Think of slicing a pizza: cutting it into 8 slices and taking 2 is the same as cutting it into 4 slices and taking 1. Both actions represent the same portion of the pizza. Mathematically, this means that 2/8 and 1/4 are equivalent fractions.
The Fundamental Principle: Multiplication and Division
The key to finding equivalent fractions lies in the principle of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This operation doesn't change the value of the fraction; it simply changes its representation.
Let's illustrate this with 2/8:
-
Simplifying Fractions: To find an equivalent fraction, we look for a common factor that divides both the numerator and the denominator. In the case of 2/8, both 2 and 8 are divisible by 2. Dividing both by 2 gives us:
(2 ÷ 2) / (8 ÷ 2) = 1/4
-
Expanding Fractions: Conversely, we can create equivalent fractions by multiplying both the numerator and the denominator by the same number. Let's multiply 2/8 by 2/2:
(2 × 2) / (8 × 2) = 4/16
Similarly, multiplying by 3/3 gives:
(2 × 3) / (8 × 3) = 6/24
Therefore, 1/4, 4/16, and 6/24 are all equivalent to 2/8. There are infinitely many equivalent fractions for any given fraction.
Finding the Simplest Form: Reducing Fractions
The simplest form of a fraction is when the numerator and denominator share no common factors other than 1. This is often referred to as simplifying or reducing the fraction to its lowest terms. In the case of 2/8, the simplest form is 1/4, as we’ve already seen. Finding the simplest form makes fractions easier to understand and compare.
How to Reduce Fractions:
-
Find the Greatest Common Factor (GCF): The GCF is the largest number that divides both the numerator and denominator without leaving a remainder. For 2/8, the GCF is 2.
-
Divide Both Numerator and Denominator by the GCF: Dividing both 2 and 8 by 2 results in the simplest form: 1/4.
Examples of Reducing Fractions:
- 6/12: GCF is 6. 6/12 = (6 ÷ 6) / (12 ÷ 6) = 1/2
- 15/25: GCF is 5. 15/25 = (15 ÷ 5) / (25 ÷ 5) = 3/5
- 18/24: GCF is 6. 18/24 = (18 ÷ 6) / (24 ÷ 6) = 3/4
Beyond 2/8: Practicing with Equivalent Fractions
Let's explore more examples to solidify our understanding:
Example 1: Finding equivalent fractions for 3/5
To find equivalent fractions for 3/5, we can multiply both the numerator and denominator by the same number:
- Multiply by 2: (3 × 2) / (5 × 2) = 6/10
- Multiply by 3: (3 × 3) / (5 × 3) = 9/15
- Multiply by 4: (3 × 4) / (5 × 4) = 12/20
All of these fractions – 6/10, 9/15, and 12/20 – are equivalent to 3/5.
Example 2: Simplifying 12/18
To simplify 12/18, we need to find the GCF of 12 and 18. The GCF is 6. Dividing both the numerator and denominator by 6:
(12 ÷ 6) / (18 ÷ 6) = 2/3
Thus, the simplest form of 12/18 is 2/3.
Example 3: Determining if two fractions are equivalent
Are 4/6 and 2/3 equivalent? To find out, we can simplify 4/6. The GCF of 4 and 6 is 2. Dividing both by 2 gives:
(4 ÷ 2) / (6 ÷ 2) = 2/3
Since both fractions simplify to 2/3, they are equivalent.
Applications of Equivalent Fractions in Real Life
Understanding equivalent fractions isn't just a classroom exercise; it's a practical skill with numerous applications in daily life:
-
Cooking and Baking: Recipes often call for fractions of ingredients. Knowing how to convert fractions allows you to adjust recipes easily, doubling or halving them without altering the proportions. For example, doubling a recipe that calls for 1/2 cup of sugar would require 1 cup (2/2 cup) of sugar.
-
Measurement: Whether it’s measuring fabric for sewing, calculating distances, or working on DIY projects, understanding equivalent fractions is essential for accurate measurements.
-
Financial Calculations: Working with percentages and proportions in financial matters requires a solid understanding of fractions and their equivalence.
-
Data Analysis and Representation: Interpreting data represented in fractions often necessitates finding equivalent fractions to compare and understand the data more efficiently.
Mastering Equivalent Fractions: Tips and Strategies
-
Practice Regularly: The more you practice, the more comfortable you’ll become with finding equivalent fractions and simplifying them.
-
Use Visual Aids: Drawing diagrams or using manipulatives can help visualize the concept of equivalent fractions.
-
Learn Your Times Tables: A strong understanding of multiplication and division is crucial for quickly finding equivalent fractions.
-
Break Down Complex Fractions: When dealing with larger numbers, break down the fractions into smaller, manageable parts.
Conclusion: A Foundation for Further Mathematical Exploration
Understanding equivalent fractions forms a crucial foundation for more advanced mathematical concepts. From working with decimals and percentages to tackling algebraic equations, the principles of equivalence and simplification are consistently applied. By mastering these concepts, you'll not only improve your mathematical skills but also enhance your problem-solving abilities in various aspects of life. The seemingly simple question of "Which fraction is equivalent to 2/8?" opens the door to a world of mathematical understanding and application. Remember the core principle: multiply or divide both the numerator and denominator by the same non-zero number to find equivalent fractions, and always strive to express your fraction in its simplest form.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 65 And 39
May 10, 2025
-
5 Out Of 50 As A Percentage
May 10, 2025
-
What Is 4 3 Divided By 5 3
May 10, 2025
-
Does One Ml Equal One Gram
May 10, 2025
-
What Is 25 Of 2 Million
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 2/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.